Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 97
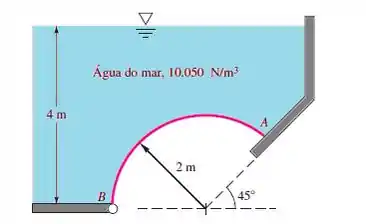
A comporta AB da figura abaixo tem três oitavos de círculo, com 3 m de largura, é articulada em B e está apoiada contra uma parede lisa em A. Calcule as forças de reação nos pontos A e B.
Passo 1
E aí gente, bora encarar mais esse problema aqui? Bora antes fazer alguns desenhos de cota na nossa figura acima!!
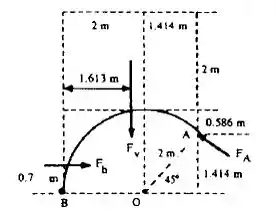
As duas forças hidrodinâmicas que atuam são:
Passo 2
Para encontrar as reações, nós vamos precisar das linhas de atuação dessas duas forças, e vamos usar nosso rascunho de cotas feitos no passo 1, beleza? O somatório dos momentos na comporta em torno de B, dará pra gente o seguinte:
Passo 3
Finalmente, o somatório das forças verticais e horizontais nos darão que:
Resposta
Exercícios de Livros Relacionados
Reconsidere o Problema 3-128. Usando o EES (ou outro aplicativo), investigue o efeito da pressão do ar acima da água sobre a força no cabo. Faça a pressão variar de 0,1 MPa até 10 MPa. Represente graf
Um contêiner cilíndrico cujo peso é de 79 N é invertido e pressionado na água, como mostra a Figura. Determine a altura diferencial h do manômetro e a força F necessária paramanter o contêiner na posi
Repita o Problema 3-59 para o caso de uma calha parcialmente cheia com água até a altura de 0,4 m diretamente acima da dobradiça.
Uma calha de água de seção transversal semicircular com raio de 0,5 m consiste em duas pares simétricas com dobradiças entre as partes inferiores, como mostra a Figura P3-58. As duas partes são mantid
Os dois lados de uma calha de água em forma de V têm dobradiças na parte inferior onde eles se encontram, como mostra a Figura P3-59, formando um ângulo de 45° com o solo em ambos os lados. Cada lado