Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 105
4.105 Um fluido com massa específica escoa ao longo de uma placa plana de largura 1 m. A velocidade da corrente livre, não perturbada, é . Em a jusante da borda de ataque da placa, a espessura da camada-limite é . O perfil de velocidade nesse local é
Trace o gráfico do perfil da velocidade. Calcule a componente horizontal da força requerida para manter a placa estacionária.
Passo 1
Vamos usar a figura do exercício anterior, pois é bem parecido.
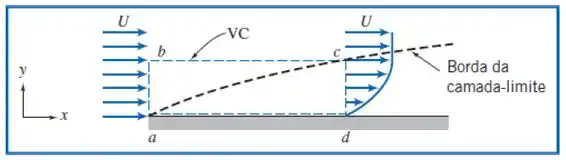
Passo 2
Vamos começar encontrando a vazão mássica que sai do volume de controle através do lado bc. Vamos usar a equação de continuidade.
Passo 3
Agora vamos usar a componente x da equação da quantidade de movimento.
Mas a força pra manter a placa estacionária é:
Resposta
Exercícios de Livros Relacionados
Uma corrente de água, na condição-padrão, sai de um bocal de 50 mm de diâmetro e atinge uma pá curva, conforme mostrado. Um tubo de estagnação conectado a um manômetro de em tubo U com água e instalad
Um bocal plano descarrega verticalmente para baixo 1200 L/s por unidade de largura na atmosfera. O bocal é alimentado com um fluxo permanente de água. Uma placa plana estacionária, inclinada, colocada
Um medidor Venturi, instalado em uma tubulação de água, consiste em uma seção convergente, uma garganta de área constante e uma seção divergente. O diâmetro do tubo é D = 100m m e o diâmetro da gargan
Dois grandes tanques contendo água têm pequenos orifícios de contornos lisos e arredondados e de áreas iguais. Um jato de líquido sai do tanque da esquerda. Considere que o fluxo seja uniforme e não a
Um jato de ar horizontal com 13 mm de diâmetro, e axialmente simétrico, atinge um disco estacionário vertical com 203 mm de diâmetro. A velocidade do jato é de 69 m/s na saída do bocal. Um manômetro e