Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 72
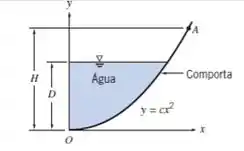
A comporta parabólica mostrada na figura tem 2 metros de largura e é articulada em ; , e . Determine (a) o módulo e a linha de ação da força vertical sobre a comporta causada pela água, (b) a força horizontal aplicada em requerida para manter a comporta em equilíbrio, e (c) a força vertical aplicada em requerida para manter a comporta em equilíbrio.
Passo 1
Letra a)
Encontrando a coordenada no ponto da seguinte maneira:
A água está a uma altura de do fundo da comporta.
Substituindo a por , na extremidade mais à direita, temos:
Calculando :
Integrando:
Sendo:
;
;
;
;
.
Temos:
Passo 2
Calculando a linha de ação da força vertical:
Integrando:
Substituindo os dados:
Passo 3
Calculando a força horizontal que atua na comporta devido à água:
é o centro da comporta.
A comporta parabólica está na forma retangular.
O centro da área retangular fica na altura da da parte inferior da comporta.
Substituindo :
Substituindo os dados:
Calculando a linha de ação dessa força horizontal na comporta:
Passo 4
Letra b)
Desenhando o diagrama de forças da comporta:
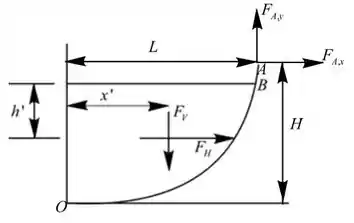
Calculando a força horizontal necessária em para manter a comporta em equilíbrio.
Analisando momento sobre o ponto .
Sendo , substituindo os dados, temos:
Desse modo, a força horizontal aplicada em A deve ser de .
Passo 5
Letra c)
Calculando a distância de força vertical ao ponto .
A distância se dá na coordenada em .
Substituindo por e para na equação da parábola:
Substituindo os dados:
Calculando a força vertical necessária em A para manter o equilíbrio.
Tomando o momento sobre o ponto :
Substituindo os dados:
Assim, a força vertical aplicada em A deve ser .