Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 115

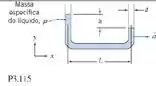
Um acelerômetro rudimentar pode ser feito com um tubo em U cheio de líquido, conforme mostrado. Deduza uma expressão para a diferença de nível h, causada por uma aceleração , em termos, da geometria do tubo e das propriedades do fluido.

Passo 1

A questão descreve um acelerômetro com tubo em U, vamos encontrar uma expressão que descreva a aceleração em termos de h e L . Portanto, aplicaremos as equações hidrostáticas nas direções x e y que são:

- ∂ p ∂ x + ρ g → x = ρ a → x

- ∂ p ∂ y + ρ g → y = ρ a → y

Fazemos as seguintes considerações: o fluido é incompressível; desprezar os cantos do tubo; e ambas as extremidades do tubo em U estão abertas para a atmosfera.

Passo 2

Analisando a figura, para a aceleração e a gravidade podemos dizer que, segundo as coordenadas: a x = a , a y = 0 , g x = 0 e g y = - g .

Dessa forma cada derivada parcial fica:

∂ p ∂ x = - ρ a e ∂ p ∂ y = - ρ g

Agora, se avaliarmos Δ p da esquerda para a direita no tubo em U, temos:

d p = ∂ p ∂ x ∂ x + ∂ p ∂ y ∂ y

Também podemos escrever esta expressão como:

∆ p = ∂ p ∂ x ∆ x + ∂ p ∂ y ∆ y

Uma vez que a derivada também pode gerar um diferencial. Logo,

∆ p = - ρ g - b + - ρ a - L + - ρ g b + h = 0

Simplificando a expressão, temos

∆ p = ρ a L + ρ g h

Isolando a altura,

h = a L g

Resposta

h = a L g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cilindro movimenta-se dentro da tubulação circular da figura com velocidade constante. A folga entre o cilindro e a tubulação contém óleo de viscosidade dinâmica μ = 10 - 2 N ⋅ s / m 2 .O peso sobre
O manômetro da figura, sabe-se que, quando a força F é 55,6k N , a leitura na régua é 100c m . Determinar o valor da nova leitura, caso a força F dobre de valor.
Um tanque fechado, com a forma indicada na figura, com 0,6m de lado, gira em torno de um eixo com rotação n = 100r p m e a uma distância radial de 1,5m . Qual é a pressão nos pontos A , B e C ? ( ρ =
The U-tube in Fig. P2.140 is moving to the right with variable velocity. The water level in the left tube is 6 cm, andthe level in the right tube is 16 cm. Determine the acceleration and its direction
A tall cylindrical container, 14 in in diameter, is used tomake a mold for forming 14-in salad bowls. The bowls areto be 8 in deep. The cylinder is half-fi lled with molten plastic, µ 5 1.6 kg/(m-s),