Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 59

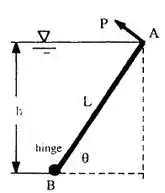
A comporta AB tem comprimento L e largura b, está articulada em B e tem peso desprezível. O nível h do líquido permanece no topo da comporta para qualquer ângulo θ . Encontre uma expressão analítica para força P, perpendicular a AB, necessária para manter a comporta em equilíbrio como mostrado abaixo.

Passo 1

O centroide da comporta está a uma distância equivalente de L/2 do ponto A e uma profundidade equivalente h/2 abaixo da superfície, certo?

Então você vai concordar comigo também que, para qualquer que seja o ângulo, a força hidrostática pode ser escrita como sendo:

F = ρ h 2 L b

Passo 2

O momento de inercia da comporta pode ser calculado usando:

I x x = ( b L 3 ) / 12  

Portanto,

y c p = I x x s e n θ h C G A = 1 12 b L 3 s e n θ h 2 L b

y c p = L 2   s e n θ 6 h

Perceba também que o centro de pressão é dado então por L / 2 - y c p partindo do ponto B. Somando então esses momentos, temos que:

∑ M i = 0

P L = F L 2 - y c p

Resolvendo, temos então:

P L = ρ h 2 L b L 2 - L 2   s e n θ 6 h

P = ρ h b 4 L - L 2 s e n θ 3 h

Resposta

P = ρ h b 4 L - L 2 s e n θ 3 h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma calha de água de seção transversal semicircular com raio de 0,5 m consiste em duas pares simétricas com dobradiças entre as partes inferiores, como mostra a Figura P3-58. As duas partes são mantid
Os dois lados de uma calha de água em forma de V têm dobradiças na parte inferior onde eles se encontram, como mostra a Figura P3-59, formando um ângulo de 45° com o solo em ambos os lados. Cada lado
Leite com densidade de 1020 kg/m³ é transportado em uma estrada plana em um tanque cilíndrico com 7 m de comprimento e 3 m de diâmetro. O caminhão-tanque é preenchido completamente com leite (sem espa
Um cilindro vertical vedado com 1,2 m de diâmetro e 3 m de altura é preenchido completamente com gasolina, cuja densidade é de 740 kg/m³. Agora o tanque é posto a girar em torno de seu eixo vertical a
Repita o Problema 3-88 para uma desaceleração de 2,5 m/s².