Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 59
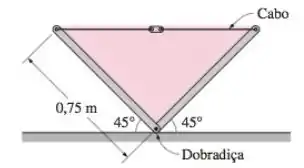
Os dois lados de uma calha de água em forma de V têm dobradiças na parte inferior onde eles se encontram, como mostra a Figura P3-59, formando um ângulo de 45° com o solo em ambos os lados. Cada lado tem 0,75 m de largura e as duas partes são mantidas unidas por um cabo e esticador colocados a cada 6 m ao longo do comprimento da calha. Calcule a tensão em cada cabo quando a calha está cheia até a borda.
Passo 1
Vamos começar pelas as hipóteses do problema em questão:
- A pressão atmosférica age em ambos os lados da comporta e por isso pode ser ignorado nos cálculos;
- O peso da calha é desprezível.
Vamos considerar a seção transversal de metade do triângulo para o diagrama de forças envolvidas nesse problema, como mostra a figura abaixo:
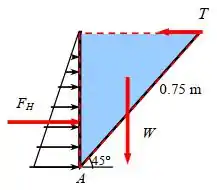
Passo 2
A força hidrostática resultante pode ser determinada a partir dos componentes horizontal e vertical e . A componente horizontal é:
A altura de água na seção transversal é:
Para esse caso, a força vertical na superfície horizontal é zero, pois coincide com superfície livre. Assim a componente vertical da força hidrostática é igual ao peso do fluido em um bloco de 6 m de comprimento:
A variável é o comprimento da superfície livre dado por:
Assim, a componente vertical é:
Passo 3
Para obtermos a tensão no cabo, vamos fazer o somatório de momentos em A. A distância das componentes da força hidrostática para a dobradiça em A equivale nesse caso ao centroide do triângulo retângulo. Assim:
Como , a tensão no cabo quando a calha está cheia é: