Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 88
Leite com densidade de 1020 kg/m³ é transportado em uma estrada plana em um tanque cilíndrico com 7 m de comprimento e 3 m de diâmetro. O caminhão-tanque é preenchido completamente com leite (sem espaço para o ar) e acelera a 2,5 m/s². Se a pressão mínima do caminhão-tanque for de 100 kPa, determine a pressão máxima e sua localização.
Passo 1
Vamos começar com as hipóteses do problema em questão:
- A aceleração do caminhão-tanque permanece constante.
- O leite é um fluido incompressível.
A figura abaixo representa a dinâmica do problema:
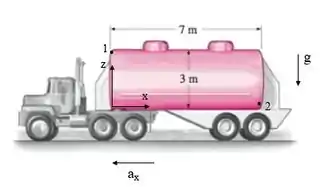
Passo 2
O caminhão está submetido a uma aceleração horizontal negativa de 2,5 m/s², pois o vetor aponta no sentido oposto ao eixo horizontal de referência (eixo x). No eixo vertical, temos ação somente da gravidade. A diferença de pressão entre dois pontos em um fluido incompressível em movimento linear é dada por:
O primeiro termo da equação resulta dos efeitos de compressão pela traseira do tanque sobre o fluido no momento que o caminhão acelera, enquanto o segundo termo é a conhecida pressão hidrostática, que aumenta com a profundidade.
Passo 3
O ponto de menor pressão será definido como 1 e o de maior pressão como 2, uma que o ponto 2 está localizado em uma profundidade maior e mais próximo à traseira do tanque. Assim, a diferença de pressão máxima no tanque é: