Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 58

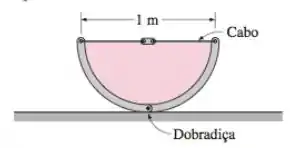
Uma calha de água de seção transversal semicircular com raio de 0,5 m consiste em duas pares simétricas com dobradiças entre as partes inferiores, como mostra a Figura P3-58. As duas partes são mantidas juntas por um cabo e esticador colocados a cada 3 m ao longo do comprimento da calha. Calcule a tensão em cada cabo quando a calha está cheia até a borda.

Passo 1

Vamos começar com as hipóteses:

A pressão atmosférica age em ambos os lados da parede e assim pode ser ignorada nos cálculos;
O peso da calha pode ser desprezado.

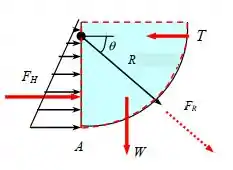
Para determinarmos a altura em cada caso, precisamos obter a força hidrostática resultante. Para isso, primeiro fazemos um diagrama de corpo livre da metade da calha:

Passo 2

A força hidrostática resultante pode ser determinada a partir dos componentes horizontal e vertical e . A componente horizontal é:

Para esse caso, a força vertical na superfície horizontal é zero, pois coincide com superfície livre. Assim a componente vertical da força hidrostática é igual ao peso do fluido em um bloco de 3 m de comprimento:

A intensidade e a direção da força hidrostática resultante são:

Passo 3

Para obtermos a tensão no cabo quando a calha está cheia, fazemos o somatório de momentos em A entre a força resultante e a tensão do cabo:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o cilindro semicircular CDE no Exemplo 2.9, encontre a força hidrostática vertical integrando o componente vertical da pressão sobre a superfície de θ = 0 até θ = π .

Uma barragem de concreto (d = 2,5) é construída na forma de um triângulo isósceles, como na Figura P2.80. Analise essa geometria para encontrar o intervalo de ângulos θ para o qual a força hidrostátic

A barragem na Figura P2.82 é um quarto de círculo com largura de 50 m. Determine os componentes horizontal e vertical da força hidrostática contra a barragem e o ponto CP em que a resultante atinge a

A comporta AB na Figura P2.83 é um quarto de círculo de 3 m de largura, articulada em B. Encontre a força F suficiente apenas para impedir que a comporta se abra. A comporta é uniforme e pesa 13.350 N

Determine (a) a força hidrostática total sobre a superfície curva AB da Figura P2.84 e (b) sua linha de ação. Despreze a pressão atmosférica e considere a superfície com largura unitária.