Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 16

Um conduto de ferro fundido de 1000 m de comprimento e 10 cm de diâmetro liga dois reservatórios em níveis constantes, e foi projetado para uma vazão de 20 L/s de água. Colocada em funcionamento a instalação, verificou-se que a vazão que circulava era igual à metade da prevista, em virtude de uma obstrução do escoamento por material esquecido no interior da tubulação. Qual é a perda de carga singular introduzida pela obstrução? Dados: γ á g u a = 10 4   N / m 3 ; μ á g u a = 10 - 3   N . s / m 2 .

Passo 1

Vamos começar o exercício calculando a velocidade do escoamento nas duas condições, na normal e com a obstrução, então, para a situação normal, temos:

Q = v A → v = Q A = Q π D 2 4 = 20.10 - 3 π 0,1 2 4 → v = 2,55   m / s

E agora para o sistema com a obstrução:

Q ' = v ' A → v ' = Q ' A = Q ' π D 2 4 = 1 0.10 - 3 π 0,1 2 4 → v ' = 1,27   m / s

Agora, aplicando o equilíbrio de energia para o sistema na condição normal, temos:

H 0 = H 1 + H p 0,1

v 0 2 2 g + p 0 γ + z 0 = v 1 2 2 g + p 1 γ + z 1 + H p 0,1

Substituindo os valores conhecidos (lembrando que são dois reservatórios em 0 e 1, então as pressões e velocidades são nulas), ficamos com:

0 2 2 g + 0 γ + z 0 = 0 2 g + 0 γ + z 1 + f L v 2 2 g D H → z 0 - z 1 = f L v 2 2 g D H

E, agora, aplicando o equilíbrio de energia para o sistema com obstrução:

H 0 = H 1 + H p 0,1 '

v 0 2 2 g + p 0 γ + z 0 = v 1 2 2 g + p 1 γ + z 1 + H p 0,1 '

Substituindo os valores conhecidos (lembrando que agora temos uma perda localizada h s ), ficamos com:

0 2 2 g + 0 γ + z 0 = 0 2 g + 0 γ + z 1 + f ' L v ' 2 2 g D H + h s → z 0 - z 1 = f ' L v ' 2 2 g D H + h s

Passo 2

Então, podemos igualar as duas expressões contendo z 0 - z 1 , obtendo:

f L v 2 2 g D H = f ' L v ' 2 2 g D H + h s

Dessa forma, precisamos encontrar o fator de atrito para os dois casos, então, calculando o número de Reynolds para ambos os casos, temos:

R e = v D ν = 2,55 0,1 10 - 6 → R e = 2,55.10 5

R e ' = v ' D ν = 1,27 0,1 10 - 6 → R e ' = 1,27 . 10 5

E, agora, vamos calcular o termo D H / k , que será o mesmo para ambos os casos (lembrando que o valor de k foi retirado do quadro dentro do diagrama de Moody a seguir, já que nos foi fornecido o material da tubulação no enunciado):

D H k = 0,1 2,59.10 - 4 → D H k = 386

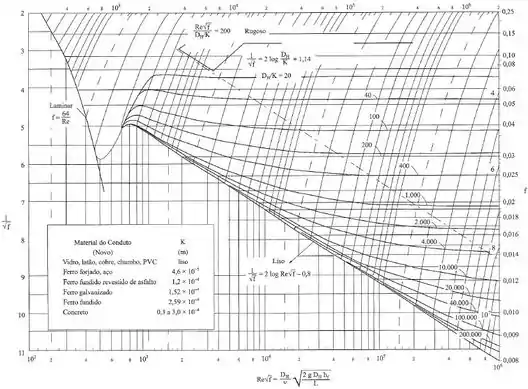
Então, com o valor de D H / k e de Reynolds, podemos encontrar no diagrama de Moody os fatores de atrito, que serão:

f = 0,026

f ' = 0,027

Passo 3

Agora podemos voltar à equação obtida no passo 1:

f L v 2 2 g D H = f ' L v ' 2 2 g D H + h s

E, substituir os valores conhecidos:

0,026 1000 2,55 2 2 10 0,1 = 0,027 1000 1,27 2 2 10 0,1 + h s → h s = 62,7   m

Resposta

h s = 62,7   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um grande reservatório fornece água para a comunidade. Uma parte do sistema de abastecimento de água é mostrada. A água é bombeada de um reservatório para um grande tanque de armazenagem antes de ser
Uma bomba está localizada 4,5 m para o lado e 3,5 m acima de um reservatório. Ela foi projetada para uma vazão de 6 L s . Para operação satisfatória, a pressão estática manométrica na aspiração da bom
Ar a 20°C escoa em uma seção quadrada de um duto feito de aço comercial. O duto tem 25 m de comprimento. Que tamanho de duto (comprimento de um lado) deve ser empregado para produzir uma vazão de 2 m
O problema 8.171 descreve uma situação na qual o escoamento em uma longa tubulação, partindo de um tanque elevado, é lentamente reduzido para evitar um aumento grande de pressão (golpe de aríete). Est
Derivados de petróleo são transportados a longas distâncias por uma tubulação como, por exemplo, a tubulação do Alasca (veja o Exemplo 8.6). Estime a energia necessária para bombear um derivado de pet