Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 13
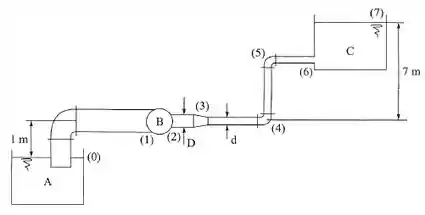
A instalação da figura será utilizada para o transporte de 12 L/s de água do reservatório A para o reservatório C, ambos mantidos em nível constante. A bomba será adquirida do fabricante X, que produz bombas de potência nominal: 0,5 CV; 1 CV; 1,5 CV; 2 CV; 3 CV; 4 CV; 5 CV, todas com rendimento de 82%. Dados: ; ;. Desprezam-se as perdas entre as seções (0) e (1). Selecionar a bomba apropriada.
Passo 1
Beleza! Então vamos começar aplicando o equilíbrio de energia ao sistema entre os pontos 0 e 7:
Substituindo os valores conhecidos, ficamos com:
Então, para encontrar a carga da bomba, e depois a sua potência, precisamos primeiro encontrar a perda de carga do sistema entre os pontos 0 e 7. Nesse exercício, temos perda distribuída e localizada, então, a perda de carga pode ser escrita como:
Observe que nesse caso tivemos que separar as perdas distribuídas, pois não temos o mesmo diâmetro de tubo durante toda a tubulação.
Passo 2
Agora precisamos encontrar os valores para substituir na equação anterior. Vamos começar encontrando as velocidades nos trechos com o auxílio da vazão:
Agora, vamos calcular o valor do número de Reynolds para cada um dos trechos:
Passo 3
Como não temos o valor de , devemos recorrer ao diagrama de Moody a seguir, para isso precisamos encontrar o valor de para os dois trechos, nesse caso, como temos uma seção circular, então e , e as equações se tornam:
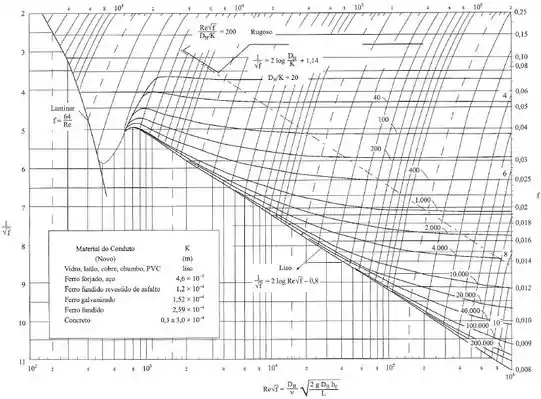
Para esses valores de e os valores de Reynolds encontrados no passo 2, o escoamento é rugoso em ambos os trechos da tubulação, que é a parcela onde as curvas possuem um valor constante (ocorrem para altos valores de ), dessa forma, para a relação encontrada, vamos adotar:
Passo 4
Agora vamos retornar à equação de equilíbrio de perda de carga do passo 1:
Substituindo os valores conhecidos, temos:
Agora substituindo esse valor na equação do passo 1 para a carga da bomba, temos:
Agora podemos aplicar a equação da potência para a bomba, dada por:
E, agora só precisamos converter a potência de para , podemos fazer isso dividindo a expressão por 735,5, pois 1 CV = 735,5 W:
Então, devemos selecionar a bomba de 2 CV para atender a demanda do problema.