Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 21
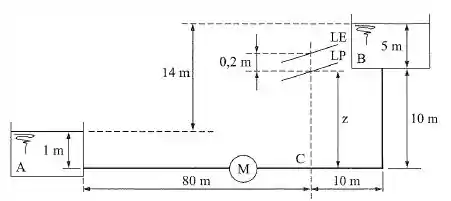
Na instalação da figura, o sistema que interliga os reservatórios A e B é constituído por uma tubulação de diâmetro constante , comprimento total e pela máquina M. Admitindo-se desprezíveis as perdas de carga singulares na tubulação e sendo conhecidos os trechos da LP e LE, como é indicado na seção C, determinar:
a) o tipo de máquina M;
b) a potência da máquina, cujo rendimento é de 75%;
c) a cota z da LP na seção indicada na figura.
Dados: ; ; ; tubo de ferro fundido.
Passo 1
A primeira coisa que devemos fazer é notar o sentido do escoamento, que pode ser identificado através do decaimento das linhas, então, o escoamento vai de B para A, dessa forma, aplicando a equação de equilíbrio de energia entre os pontos B e A, temos:
Agora, substituindo os valores conhecidos, temos:
Então precisamos encontrar o valor da perda de carga do sistema, para isso, vamos começar encontrando a velocidade através da diferença de energia para a linha piezométrica, sabendo que:
Passo 2
Como vamos precisar o diagrama de Moody para descobrir o valor de , então vamos precisar do valor de Reynolds, que será:
Agora precisamos encontrar o valor da relação , nesse caso, como a seção do tubo é circular e uniforme, então , e para encontrar o valor de do ferro fundido, vamos recorrer ao quadro dentro do diagrama de Moody a seguir:
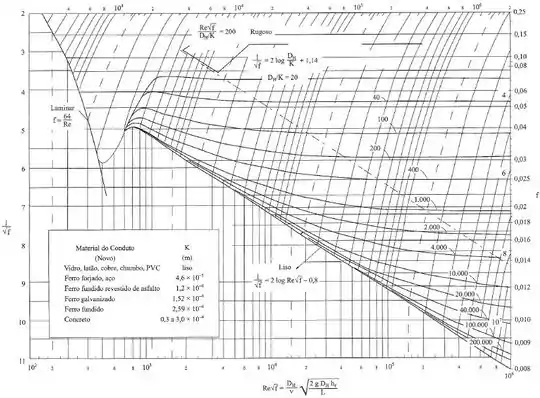
Então, para os valores de e Reynolds encontrado, podemos pegar um valor na parte totalmente rugosa do diagrama de Moody, então teremos:
Dessa forma, sabemos que a perda de carga distribuída será dada por:
Substituindo esse valor para a carga da máquina obtida no passo 1, temos:
Como a carga da máquina é negativa, temos então uma turbina.
Passo 3
Agora para resolver a letra b), precisamos primeiro encontrar a vazão no sistema, então:
Agora podemos aplicar a equação da potência para uma turbina:
Passo 4
Agora para encontrar a cota da LP no ponto C, que é dado por , vamos aplicar o equilíbrio de energia entre os pontos B e C:
Substituindo os valores conhecidos, temos: