Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 3.Problemas - Ex. 34
Um cone sólido truncado tem seção transversal circular e seu diâmetro está relacionado à coordenada axial por uma expressão da forma , onde .
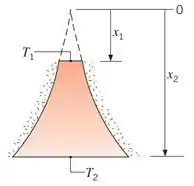
Os lados são bem isolados, enquanto a superfície superior do cone em é mantida em e a superfície inferior em é mantida em .
(a) Obtenha uma expressão para a distribuição de temperatura .
(b) Qual é a taxa de transferência de calor através do cone se ele for construído de alumínio puro com , , , e ?
Passo 1
Fala galera!! Vem comigo fazer mais uma questão!!
Para resolver essa questão, podemos começar fazendo as seguintes suposições:
(1) Condições de estado estacionário.
(2) Condução unidimensional em .
(3) Propriedades constantes.
Propriedades;
Pela Tabela A-1 a .
Condutividade térmica do Alumínio: .
Passo 2
(a) Para resolver essa questão, podemos usar a ideia de que a condução de calor ocorre em condições unidimensionais, em estado estacionário, e não há geração interna de calor, a taxa de transferência de calor é uma constante independente de . Nesse contexto, a lei de Fourier, Equação 2.1, com
pode ser usada para determinar a distribuição de temperaturas. Assim, temos que:
Portanto, uma vez que é independente de ,
Portanto:
Passo 3
(b) Usando a relação obtida no passo anterior, temos que a taxa de transferência de calor é a seguinte:
Substituindo os termos da expressão acima pelos dados fornecidos, temos:
Portanto, a taxa de transferência de calor é .
Resposta
(a)
(b)