Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 18

18. Um engenheiro deseja medir a condutividade térmica de um material na forma de aerogel. Espera-se que o aerogel tenha uma condutividade térmica extremamente pequena.

(a) Explique por que o aparelho do Problema 2.17 não pode ser usado para obter uma medida precisa da condutividade térmica do aerogel.

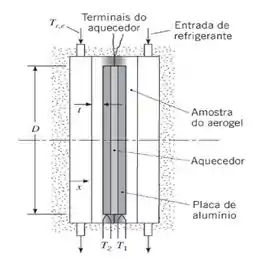
(b) O engenheiro projeta um novo aparelho no qual um aquecedor elétrico, de diâmetro D = 150 mm, é incluso entre duas placas finas de alumínio. As temperaturas, T1 e T2, das duas placas de alumínio com 5 mm de espessura, são medidas no regime estacionário com termopares. Folhas do aerogel, com espessura t = 5 mm, são posicionadas pelo lado externo das placas de alumínio, enquanto um refrigerante com uma temperatura de entrada Tr,e = 25°C mantém as superfícies exteriores do aerogel a uma temperatura baixa. As folhas circulares de aerogel são feitas de tal forma que elas envolvam o aquecedor e as placas de alumínio, proporcionando isolamento para minimizar as perdas térmicas radiais. No regime estacionário, T1 = T2 = 55°C e passam no aquecedor 125 mA a 10 V. Determine o valor da condutividade térmica do aerogel, ka.

(c) Calcule a diferença de temperaturas ao longo da espessura das placas de alumínio de 5 mm. Comente se é importante o conhecimento das posições axiais nas quais as temperaturas das placas de alumínio são medidas.

(d) Sendo água líquida usada como refrigerante a uma vazão total de = 1 kg/min (0,5 kg/min para cada uma das duas correntes), calcule a temperatura de saída da água, Tr,s.

Passo 1

Letra (a)

O aparelho no problema 2.17 não pode ser usado porque se considera que a transferência de calor ocorre em uma dimensão. Embora o aerogel usado tenha menos condutividade térmica quando comparado ao isolamento usado no aparelho pelo qual as perdas de calor radial são consideráveis ​​e não podem ser negligenciadas. Portanto, não podemos usar o aparelho para medir a condutividade térmica do aerogel.

Passo 2

Letra (b)

Calcule a energia elétrica gerada no aparelho.

E ˙ g = V I

E ˙ g = 10 × 125 × 10 - 3

= 1,25   W

Calcule o calor conduzido através de cada camada de aerogel.

q ˙ = E g 2

q ˙ = 1,25 2

= 0,625   W

Calcule o calor conduzido através de cada camada de aerogel usando a lei de Fourier de condutividade térmica.

q ˙ = - k a A d T d x

= - k a π D 2 4 T e n t r a d - T a q u e c e d o r e

0,625 = - k a π × 0,15 2 4 25 - 55 0,005

0,625 = 106 k a

k a = 5,89 × 10 - 3 W m . K

Portanto, a condutividade térmica do aerogel é  5,89 × 10 - 3 W m . K .

Passo 3

Letra (c)

Calcule a diferença de temperatura entre as placas de alumínio, igualando o fluxo de calor de alumínio e aerogel.

- k a T e n t r a d a - T a q u e c e d o r e = - k a l ∆ T a l e

- 5,89 × 10 - 3 × 25 - 55 0,005 = - 239 × ∆ T a l 0,005

∆ T a l = 0,74 × 10 - 3   ° C

Portanto, a diferença de temperatura entre as placas é  0,74 × 10 - 3   ° C .

Passo 4

Letra (d)

Calcule a temperatura de saída da água considerando que o calor gerado pelo aquecedor é retirado pela água.

E g = m c p T s a í d a - T e n t r a d a

T s a í d a = T e n t r a d a + E g m c p

T s a í d a = 25 + 1,25 1 k g m i n × 1 60 m i n s × 4180

T s a í d a = 25,02   ° C

Portanto, a temperatura de saída da água é  25,02 ° C .

Resposta

  1. Explicação em texto
  2. k a = 5,89 × 10 - 3 W m . K
  3. ∆ T a l = 0,74 × 10 - 3   ° C
  4. T s a í d a = 25,02   ° C
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

11. Considere condições de regime estacionário na condução unidimensional em uma parede plana com uma condutividade térmica k = 50 W/(m · K) e espessura L = 0,25 m, sem geração interna de calor.Determ
17. Um aparelho para medir condutividade térmica emprega um aquecedor elétrico que é posicionado entre duas amostras idênticas, com 30 mm de diâmetro e 60 mm de comprimento, que são pressionadas entre
Considere as distribuições de temperaturas em regime estacionário no interior de uma parede composta pelos Materiais A e B para os dois casos mostrados. Não há geração interna e o processo de condução
Considere uma parede plana unidimensional com espessura 2 L . A superfície em x=- L é submetida a condições de convecção caracterizadas por T ∞ , 1eh 1 , enquanto a superfície em x=+ L é submetida a c
A parede plana mostrada na figura, com propriedades constantes e sem geração interna de calor, está inicialmente a uma temperatura uniforme T i . De repente, a superfície emx=L é aquecida por um fluid