Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 12

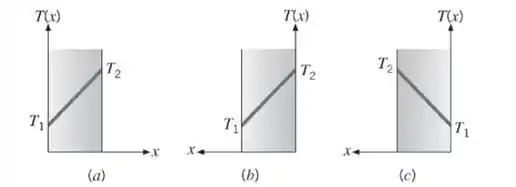
12. Considere uma parede plana com 100 mm de espessura e condutividade térmica igual a 100 W/(m · K). Sabe-se que há condições de regime estacionário quando T1 = 400 K e T2 = 600 K. Determine o fluxo térmico e o gradiente de temperatura dT/dx para os sistemas de coordenadas mostrados.

Passo 1

Letra (a)

Encontre o valor do gradiente de temperatura da seguinte maneira:

d T d x = T 2 - T 1 L     ( 1 )

d T d x = 600 - 400 0,1

d T d x = 2000 K m

Portanto, o gradiente de temperatura é 2000 K m .

O fluxo de calor é determinado da seguinte maneira:

q x ' ' = - k d T d x ( 2 )

q x ' ' = - 100 × 2000

q x ' ' = - 200 k W m 2

Portanto, o fluxo de calor é - 200 k W m 2 .

Passo 2

Letra (b)

Encontre o valor do gradiente de temperatura da seguinte maneira:

d T d x = T 2 - T 1 L     ( 1 )

d T d x = 600 - 400 - 0,1

d T d x = - 2000 K m

Portanto, o gradiente de temperatura é - 2000 K m .

O fluxo de calor é determinado da seguinte maneira:

q x ' ' = - k d T d x ( 2 )

q x ' ' = - 100 × ( - 2000 )

q x ' ' = 200 k W m 2

Portanto, o fluxo de calor é 200 k W m 2 .

Passo 3

Letra (c)

Encontre o valor do gradiente de temperatura da seguinte maneira:

d T d x = T 2 - T 1 L     ( 1 )

d T d x = - ( 600 - 400 ) - 0,1

d T d x = 2000 K m

Portanto, o gradiente de temperatura é 2000 K m .

O fluxo de calor é determinado da seguinte maneira:

q x ' ' = - k d T d x ( 2 )

q x ' ' = 100 × ( 2000 )

q x ' ' = 200 k W m 2

Portanto, o fluxo de calor é 200 k W m 2 .

Resposta

  1. d T d x = - 2000 K m         q x ' ' = - 200 k W m 2
  2. d T d x = - 2000 K m         q x ' ' = 200 k W m 2
  3. d T d x = 2000 K m         q x ' ' = 200 k W m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9. É solicitado a um jovem engenheiro o projeto de uma barreira para proteção térmica de um dispositivo eletrônico sensível, que pode vir a ser exposto à irradiação de um laser de alta potência. Tendo
15. Considere a geometria do Problema 2.14 para o caso no qual a condutividade térmica varia com a temperatura na forma k = ko + aT, na qual ko = 10 W/(m· K), a = −10−3 W/(m · K2), e T está em kelvins
13. Um cilindro com raio ro, comprimento L e condutividade térmica k está imerso em um fluido com coeficiente de transferência de calor por convecção h e temperatura desconhecida T∞. Em certo instante
16. Condução de calor unidimensional, em regime estacionário, ocorre em uma barra de condutividade térmica constante k e área da seção transversal variando conforme a relação Ax(x) = Aoeax, na qual Ao
14. No corpo bidimensional mostrado na figura, sabe-se que o gradiente de temperatura na superfície A é ∂T/∂y = 30 K/m. Quais são os valores dos gradientes ∂T/∂y e ∂T/∂x na superfície B?