Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 7.Problemas - Ex. 17

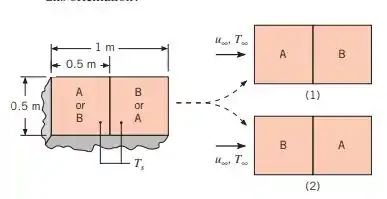
A superfície superior de um compartimento aquecido possui uma porção muito lisa ( A ) e outra acentuadamente rugosa ( B ) , e encontra-se em contato com uma corrente de ar atmosférico. Com o interesse de minimizar a transferência de calor por convecção total na superfície, qual das duas orientações, ( 1 ) ou ( 2 ) , é preferível? Se T s = 10 ° C , T ∞ = 35 ° C e u ∞ = 25   m / s , qual é a taxa de transferência de calor por convecção em toda a superfície para essa orientação?

Passo 1

Opa, como é que tá?

Pronto para resolver essa questão comigo?

Vamos lá então!

Começamos o nosso problema obtendo algumas propriedades do ar sob a temperatura de filme:

T f = 10 + 35 2 = 22,5 ° C = 295,5   K

Pela Tabela A.4, aproximando para 300   K :

v = 15,89 × 10 - 6   m 2 / s

k = 0,0263   W / m ⋅ K

P r = 0,707

Bora para os cálculos!

Passo 2

Agora, devemos calcular o número de Reynolds:

R e ∞ = u ∞ L v = 25 ⋅ 1 15,89 × 10 - 6 = 1,57 × 10 6

R e g i m e   T u r b u l e n t o !

Assim, na configuração 1, uma transição ocorrerá imediatamente antes da superfície rugosa ( x c = 0,48   m ) , temos então:

N u - L , 1 = 0,037 ⋅ R e ∞ 4 5 - 871 ⋅ P r 1 3

N u - L , 1 = 0,037 ⋅ 1,57 × 10 6 4 5 - 871 ⋅ 0,707 1 3

N u - L , 1 = 2208

Para a configuração 2:

N u - L , 2 = 0,037 ⋅ R e ∞ 4 5 ⋅ P r 1 3

N u - L , 2 = 0,037 ⋅ 1,57 × 10 6 4 5 ⋅ 0,707 1 3

N u - L , 2 = 2983,5

Assim:

N u - L , 2 > N u - L , 1

Então, utilizaremos a configuração 1 de base.

Passo 3

Calculando o coeficiente convectivo:

N u - L , 1 = h - L , 1 L k = 2208

h - L , 1 = 2208 k L

h - L , 1 = 2208 ⋅ 0,0263 1

h - L , 1 = 58,1   W / m 2 ⋅ K

Por fim, calculando a taxa de transferência de calor:

q 1 = h - L , 1 A T s - T ∞

q 1 = 58,1 ⋅ 0,5 ⋅ 1 ⋅ 35 - 10

q 1 = 726,25   W

E aí, foi de boa né?

Te espero na próxima questão!

Resposta

q 1 = 726,25   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as mesmas condições iniciais, pode-se esperar que a camada limite laminar térmica e a camada limite de quantidade de movimento tenham a mesma espessura quando o número de Prandtl do escoamento é
Seja o escoamento sobre uma placa plana no qual se deseja determinar o coeficiente de transferência de calor médio em uma pequena seção entre x 1 e x 2 , h - 1 - 2 , sendo x 2 - x 1 ≪ L .Forneça três
Uma placa plana, com largura de 1m , é mantida a uma temperatura superficial uniforme de T s = 150 ° C pelo uso de módulos retangulares geradores de calor, com espessura a = 10m m e comprimento b = 50
Seja o perfil de velocidade na camada-limite de velocidade sobre uma placa plana representado por u = C 1 + C 2 y . Utilizando condições de contorno apropriadas, obtenha uma expressão para o perfil de
Um aquecedor elétrico de ar é constituído por um conjunto horizontal de finas tiras metálicas que possuem, cada uma, 10m m de comprimento na direção do escoamento do ar, que é paralelo à superfície su