Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 81

Para a configuração de escoamento da Fig. 8.12, é sabido que a perda de carga é 1 m. Da entrada para a saída, a queda de pressão é 50 kPa, a velocidade dobra da entrada para a saída, e o aumento de elevação é de 2 m. Calcule a velocidade de entrada da água.

Passo 1

Considerando a Figura a seguir, este problema buscará obter a a velocida com que a água entra na seção 1.

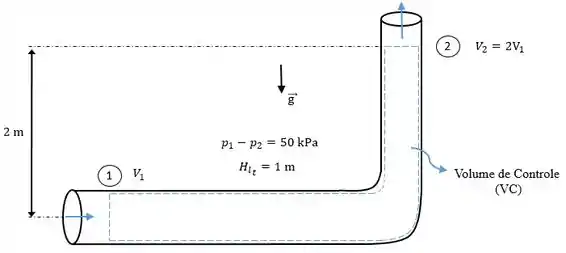
Para isso será utilizada a Equação de Energia, a ser aplicada entre as seções 1 e 2, conforme expressão:

p 1 ρ 1 g + α V 1 2 2 g + z 1 = p 2 ρ 2 g + α V 2 2 2 g + z 2 + H l t

Para a aplicação da equação apresentada, as seguintes hipóteses são necessárias:

- regime permanente ( ∂ / ∂ t = 0 );

- escoamento incompressível ( ρ 1 = ρ 2 ,   ) e de água ( ρ = 1000   k g / m ³ );

- fator de correção α ≈ 1,0 (o problema não especificou tal parâmetro, logo adotaremos o valor de 1, o qual é característico de escoamento turbulento em tubos);

- queda de pressão p 1 - p 2 = 50   k P a ;

- perda de carga H l t = 1   m ;

- diferença de nível z 2 - z 1 = 2   m ;

- velocidade na saída (seção 2) o dobro da velocidade da entrada ( V 2 = 2 V 1 ).

Passo 2

A partir da Equação da Energia e buscando isolar a velocidade na seção de entrada da tubulação:

p 1 ρ 1 g + α V 1 2 2 g + z 1 = p 2 ρ 2 g + α V 2 2 2 g + z 2 + H l t

α V 1 2 2 g - α V 2 2 2 g = p 2 ρ g - p 1 ρ g + z 2 - z 1 + H l t

Sabendo que α ≈ 1,0 , então:

V 1 2 - V 2 2 2 g = p 2 - p 1 ρ g + ( z 2 - z 1 ) + H l t

V 1 2 - 2 V 1 2 2 g = p 2 - p 1 ρ g + ( z 2 - z 1 ) + H l t

V 1 2 - 4 V 1 2 2 g = p 2 - p 1 ρ g + ( z 2 - z 1 ) + H l t

- 3 V 1 2 2 g = p 2 - p 1 ρ g + ( z 2 - z 1 ) + H l t

Rearranjando a expressão:

3 V 1 2 2 g = p 1 - p 2 ρ g - z 2 - z 1 - H l t

3 V 1 2 2 g = p 1 - p 2 ρ g - z 2 - z 1 - H l t

V 1 2 = 2 3 ( p 1 - p 2 ) ρ - g z 2 - z 1 - g H l t

Então, a velocidade na seção de entrada é dada por:

V 1 = 2 3 ( p 1 - p 2 ) ρ - g z 2 - z 1 - g H l t

Passo 3

Utilizando os valores dos parâmetros conhecidos na expressão de V 1 , tem-se que:

V 1 = 2 3 50 × 10 3 1000 - 9,81 × 2 - 9,81 × 1

Então, a velocidade na entrada da tubulação vale:

V 1 = 3,70   m / s

Resposta

V 1 = 3,70   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O perfil adimensional de velocidade para escoamento laminar completamente desenvolvido entre placas paralelas infinitas, com a placa superior se movendo com velocidade constante U , é mostrado na Fig.
Considere o escoamento laminar, permanente, completamente desenvolvido de um líquido viscoso para baixo sobre uma superfície inclinada sem gradiente de pressão. O perfil de velocidade foi deduzido no
Um mancal de deslizamento selado é formado por cilindros concêntricos. O raio interno e o externo são 25 e 26 mm, respectivamente, o comprimento do mancal é 100 mm, e ele gira a 2800 rpm. A folga radi
Considere o escoamento laminar, permanente, completamente desenolvido de um fluido viscoso para baixo sobre uma superfície inclinada. A camada de líquido tem espessura constante, h . Utilize um volume
Líquido viscoso, com vazão volumétrica Q , é bombeado através da abertura central para dentro da folga estreita entre os discos paralelos mostrados. A vazão é baixa, de modo que o escoamento é laminar