Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 94
Dois discos circulares, de raio R, estão separados pela distância . O disco superior se move em direção ao inferior com uma velocidade constante . O espaço entre eles está cheio de um líquido sem atrito, não viscoso, que é esguichado para fora quando os discos se encontram. Considere que a velocidade é uniforme em qualquer seção radial através da fresta de largura . Entretanto, note que é uma função do tempo. A pressão em torno dos discos é a atmosférica. Determine a pressão manométrica em .
Passo 1
Vamos começar o exercício ilustrando o problema descrito no enunciado:
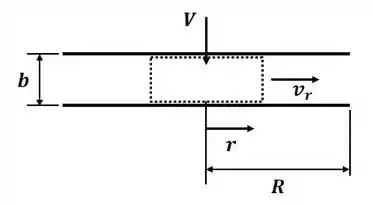
Vamos começar esse exercício aplicando a equação para a quantidade de movimento para o sistema na direção , então, temos:
Então, nesse exercício, não temos nenhuma força de superfície agindo sobre o sistema na direçao , então Também podemos desconsiderar as forças gravitacionais na direção , então . Nesse caso, sabemos que podemos escrever o volume do volume de controle como:
E a área como:
Então, a equação da quantidade de movimento se torna:
Como o único termo que depende do tempo é , então:
No entanto, sabemos que a variação de com o tempo, nada mais é do que a velocidade de aproximação do disco superior, então:
Então a equação se torna:
Passo 2
Agora vamos aplicar a equação de Bernoulli para regime transiente entre um ponto a uma distância do centro (ponto 1) e a extremidade dos discos em (ponto 2), então, temos:
Nesse caso, como o ponto 2 está exposto à atmosfera, temos . Podemos desprezar a diferença entre as cotas e . Sabemos também que o trajeto será percorrido na direção , então temos . Sabemos também que e que . Dessa forma, a equação se torna:
Agora, substituindo a expressão encontrada para no passo 1, temos:
Resolvendo a derivada, lembrando de aplicar a regra da cadeia, pois depende do tempo, temos:
Só que como vimos no passo 1:
Substituindo esse valor na expressão anterior:
Passo 3
Substituindo o valor encontrado para a derivada na equação de Bernoulli, temos:
Substituindo os valores para e e resolvendo a integral, temos:
Substituindo os limites de integração, temos:
Passo 4
Como o enunciado nos pediu para encontrar a pressão manométrica em , vamos substituir esse valor de na última equação do passo 3 e também fazer para obter uma pressão manométrica, então, temos: