Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 29

Considere o escoamento laminar, permanente, completamente desenvolvido de um líquido viscoso para baixo sobre uma superfície inclinada sem gradiente de pressão. O perfil de velocidade foi deduzido no Exemplo 5.9. Trace o perfil de velocidade. Calcule a viscosidade cinemática do líquido, se a espessura do filme com inclinação de 30° for 0,8 mm e a velocidade máxima 15,7 mm/s.

Passo 1

Tá legal, a primeira coisa que devemos fazer é pegar a equação do perfil de velocidade do Exemplo 5.9 do livro, então, recorrendo ao capítulo 5, temos:

u = ρ g s e n θ μ h y - y 2 2

Agora, sabemos que a viscosidade cinemática é dada por:

ν = μ ρ

Então, a equação para o perfil de velocidade se torna:

u = g s e n θ ν h y - y 2 2

Passo 2

E, nós sabemos que a velocidade máxima se dará na placa superior, então, a nossa condição de contorno será:

y = h → u = u m á x

Substituindo esses valores na expressão para o perfil de velocidade, temos:

u m á x = g s e n θ ν h 2 - h 2 2 → u m á x = g h 2 s e n θ 2 ν → ν = g h 2 s e n θ 2 u m á x

Então, substituindo os valores conhecidos nessa expressão, chegamos em:

ν = 9,81 0,8.10 - 3 2 s e n 30 ° 2 15,7.10 - 3 → ν = 1.10 - 4   m 2 / s

Passo 3

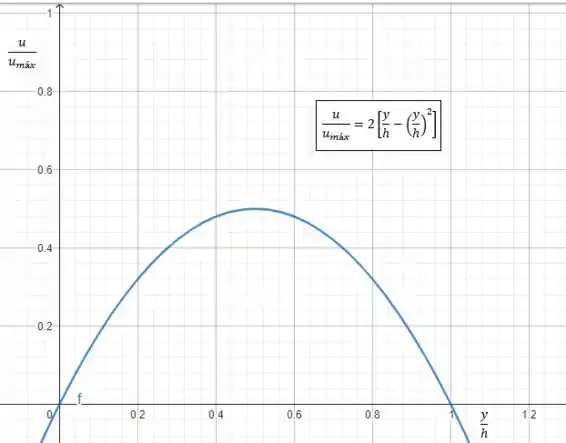
Agora, iremos plotar o perfil de velocidade adimensional, dessa forma, temos que dividir a equação do perfil de velocidade pela velocidade máxima, então, teremos:

u u m á x = g s e n θ ν h y - y 2 2 g h 2 s e n θ 2 ν → u u m á x = 2 y h - y 2 h 2

u u m á x = 2 y h - y h 2

Então, o gráfico dessa função será:

Resposta

ν = 1.10 - 4   m 2 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um macaco hidráulico suporta uma carga de 50.000 N/m por pé de comprimento perpendicular ao diagrama. O mancal é alimentado com óleo SAE 10W – 30 a 35°C e 700 kPa através do rasgo central. Como o óleo
O perfil de velocidade para escoamento completamente desenvolvido entre placas planas paralelas estacionadas é dado por u = a ( h 2 / 4 - y 2 ) , na qual a é constante, h é o espaçamento entre as plac
Água a 60 ° C escoa para a direita entre duas grandes placas planas. A placa inferior se move para a esquerda com velocidade de 0,3m / s ; a placa superior está parada. O espaçamento entre as placas é
Usando o perfil do Problema 8.18, mostre que a vazão obtida a partir da lei de potência para escoamento laminar, completamente desenvolvido, de um fluido entre placas planas paralelas pode ser escrita
Considere o escoamento laminar completamente desenvolvido entre placas paralelas infinitas espaçadas de d=10m m . A placa superior se move para a direita com velocidade U 2=0,5m / s ; a placa inferior