Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 27
O perfil adimensional de velocidade para escoamento laminar completamente desenvolvido entre placas paralelas infinitas, com a placa superior se movendo com velocidade constante , é mostrado na Fig. 8.6. Determine os gradientes de pressão em termos de , e para os quais (a) a placa superior e (b) a placa inferior experimentam tensão de cisalhamento zero. Trace um gráfico dos perfis de velocidade adimensional para estes casos.
Passo 1
Tá legal, então, o perfil adimensional de velocidade a que o enunciado se refere é mostrado a seguir:
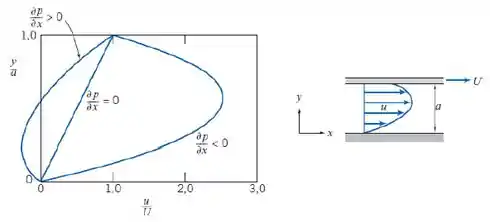
E, da equação 8.8 vista nessa seção, podemos escrever o perfil de velocidade como:
E, nós sabemos que a tensão de cisalhamento é dada por:
Então, derivando a expressão para a velocidade em , temos:
Então, substituindo essa expressão na equação para o cisalhamento, temos:
Passo 2
Então, para que a placa superior tenha tensão de cisalhamento zero, devemos ter:
Dessa forma, substituindo esses valores na equação encontrada no passo 1, temos:
Então, como vamos precisar dos perfis de velocidade, vamos substituir essa expressão na equação para a velocidade, dessa forma, temos:
Passo 3
Agora, repetindo o processo para a letra (b), onde queremos que a placa inferior tenha tensão de cisalhamento zero, de modo que:
Dessa forma, substituindo esses valores na equação encontrada no passo 1, temos:
Então, como vamos precisar dos perfis de velocidade, vamos substituir essa expressão na equação para a velocidade, dessa forma, temos:
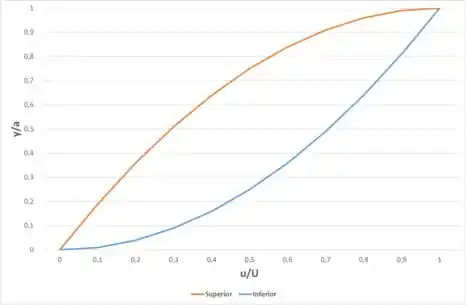
Passo 4
O gráfico para o perfil de velocidade para o caso das letras (a) e (b) estão ilustrados a seguir:
