Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 19
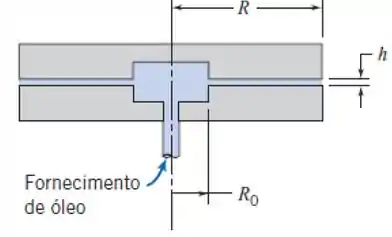
Líquido viscoso, com vazão volumétrica , é bombeado através da abertura central para dentro da folga estreita entre os discos paralelos mostrados. A vazão é baixa, de modo que o escoamento é laminar, o gradiente de pressão devido à aceleração convectiva na folga é desprezível comparado com o gradiente causado pelas forças viscosas (isto é chamado escoamento de arrasto ou creeping flow). Obtenha uma expressão geral para a variação da velocidade média no espaço entre os discos. Para escoamento de arrasto, o perfil de velocidade em qualquer seção transversal na folga é o mesmo que para escoamento completamente desenvolvido entre placas paralelas estacionárias. Avalie o gradiente de pressão como uma função do raio. Obtenha uma expressão para . Mostre que a força líquida requerida para manter a placa superior na posição mostrada é:
Passo 1
Beleza! A primeira coisa que devemos fazer é relembrar a definição de vazão em função da velocidade média, então, temos:
Agora, como vimos nessa seção na equação 8.6b, a vazão volumétrica por unidade de profundidade é dada por:
No nosso caso, temos e , então a equação se torna:
Agora vamos integrar essa expressão de até , ou seja, de até , então, teremos:
Resolvendo as duas integrais, temos:
Substituindo os valores de integração, temos:
Pela propriedade dos logarítmos, podemos escrever:
Então, a equação para será:
Passo 2
Dessa forma, agora podemos escrever a força na placa superior como:
Beleza, agora vamos utilizar pressões manométricas, de modo que , então para , integrando a expressão acima, lembrando que temos que aplicar a regra do produto, temos:
Passo 3
Resolvendo a integral restante, temos:
Então, substituindo os limites de integração, temos:
Então, substituindo essa expressão na equação para , temos:
Dessa forma, eliminando os dois termos em comum com sinais opostos , ficamos com: