Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 85

Conforme mostra o Exemplo 5.3, os dados de desempenho de uma bomba podem ser adimensionalizados. O Problema P5.61 forneceu dados adimensionais típicos para “altura manométrica” da bomba, H = ∆ p ρ g , da seguinte forma:

g H n 2 D 2 ≈ 6,0 - 120 Q n D 3 2

em que Q é a vazão volumétrica, n a rotação em r/s e D o diâmetro da hélice. Esse tipo de correlação permite calcular H quando são conhecidos ( ρ , Q, D). (a) Mostre como arranjar esses grupos pi de forma que se possa dimensionar a bomba, isto é, calcular D diretamente quando forem conhecidos (Q, H, n). (b) Faça um gráfico simples mas eficaz da sua nova função. (c) Aplique a parte (b) ao seguinte exemplo: determinar D quando H =   37   m ,   Q =   0,14 m 3 s   e   n =   35   r / s . Determine o diâmetro da bomba para essa condição.

Passo 1

Bora pra mais umaaa!!

  1. Segundo o teorema de Pi Buckingham teremos que eliminar D de um ou outro dos dois parâmetros. Vamos remover do lado esquerdo por ser o mais simples, então o novo parâmetro será:

    2. Π 3 = g H n 2 D 2 n D 3 Q 2 / 3 = g H n 4 3 Q 2 3

    n D 3 Q = f c n g H n 4 3 Q 2 3

    Com essa função, tendo (Q,H, n) obtemos imediatamente o diâmetro D.

    Passo 2

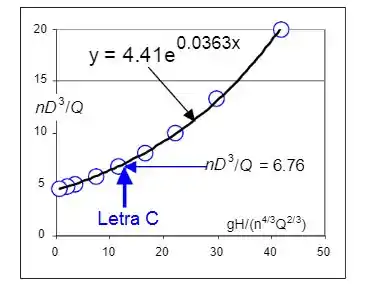
  2. A nova variável nos atrapalha muito no plotar do gráfico, em comparação da formula parabólica original. Entretanto, utilizando recursos computacionais (aqui foi utilizado o excel) é possível plotar alguns valores e descrever a curva da função, conforme será representado posterior ao item C.
  3.   Da equação abaixo, com os valores enunciados, obtemos que uma bomba de 0,3m de diâmetro satisfaz a equação.

D = f c n   g H n 4 3 Q 2 3   Q n 1 3

Resposta

  1. n D 3 Q = f c n g H n 4 3 Q 2 3

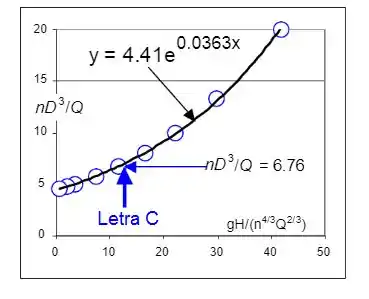
  3. O diâmetro deve ser de 30cm.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pêndulo tem um período de oscilação T que é considerado dependente do seu comprimento L, da massa m, do ângulo de balanço θ e da aceleração da gravidade g. Um pêndulo de 1m de comprimento, com uma
Com uma boa aproximação, a condutividade térmica k de um gás depende apenas da massa específica ρ , do livre caminho médio l , da constante R do gás e da temperatura absoluta T. Para o ar a 20°C e 1 a
A taxa de transferência de calor q por unidade de área para um corpo por meio de um fluido em convecção natural ou gravitacional é uma função da diferença de temperatura Δ T , da gravidade g , do comp
A força de sustentação F sobre um míssil é uma função de seu comprimento L, da velocidade V, do diâmetro D, do ângulo de ataque α , da massa específica ρ , da viscosidade μ e da velocidade do som no a
A força de propulsão F de uma hélice geralmente é considerada uma função de seu diâmetro D e da velocidade angular Ω , da velocidade V de avanço, da massa específica ρ e da viscosidade μ do fluido. Re