Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 111
Um conjunto de placas de circuitos verticais com de altura deve ser resfriado com ar de maneira que a temperatura nas placas não seja superior a , quando a temperatura do ambiente é de .
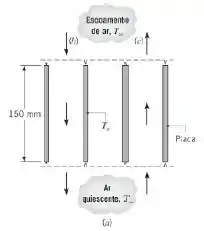
Admitindo condições de superfícies isotérmicas, determine a dissipação de potência elétrica admissível por placa nas seguintes configurações de resfriamento:
a) Somente convecção natural (nenhum escoamento forçado de ar).
b) Escoamento de ar com uma velocidade descendente de .
c) Escoamento de ar com uma velocidade ascendente de .
d) Escoamento de ar com uma velocidade (ascendente ou descente) de .
Passo 1
Começamos o problema calculando a temperatura de filme:
Sendo:
;
.
Temos:
Pela Tabela obtemos as seguintes propriedades do ar sob a temperatura de filme:
Passo 2
Letra a)
A dissipação de energia elétrica por placa pode ser expressa como:
Para o número de faces igual a 2.
Para fluxos externos livres de convecção, o número de Rayleigh é dado por:
Dados:
;
.
Temos:
O número médio de Nusselt para fluxo laminar é:
Substituindo os termos:
Sabemos que:
Substituindo os valores:
Voltando na equação de dissipação de potência elétrica:
Passo 3
Letra b)
O critério para determinarmos se a convecção livre ou forçada é dado por:
E o número de Rayleigh por:
Calculando o número de Reynolds:
Então:
O regime de convecção mista está presente.
A correlação para transferência de calor por convecção mista para fluxos externos e internos é dada por:
Com para geometria de uma placa de circuito vertical e fluxo oposto.
Como é dado por:
E por:
Temos:
Sabemos que:
Substituindo os valores:
Voltando na equação de dissipação de potência elétrica:
Passo 4
Letra c)
O critério para determinarmos se a convecção livre ou forçada é dado por:
E o número de Rayleigh por:
Calculando o número de Reynolds:
Então:
O regime de convecção forçada está presente.
A correlação para transferência de calor por convecção mista para fluxos externos e internos é dada por:
Com para geometria de uma placa de circuito vertical e fluxo de assistência.
Como é dado por:
E por:
Temos:
Sabemos que:
Substituindo os valores:
Voltando na equação de dissipação de potência elétrica:
Passo 5
Letra d)
O critério para determinarmos se a convecção livre ou forçada é dado por:
E o número de Rayleigh por:
Calculando o número de Reynolds:
Então:
O regime de convecção forçada está presente.
Como é dado por:
Sabemos que:
Substituindo os valores:
Voltando na equação de dissipação de potência elétrica: