Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 6

Considere água pressurizada, óleo de motor (não usado) e NaK ( 22 % / 78 % ) escoando em um tubo com 20 mm de diâmetro.

  1. Determine a velocidade média, o comprimento de entrada fluidodinâmico e o comprimento de entrada térmico para cada um dos fluidos, quando sua temperatura é de 366 K e a vazão mássica é de 0,01 k g s .
  2. Determine a vazão mássica, o comprimento de entrada fluidodinâmico e o comprimento de entrada térmico para a água e o óleo de motor a 300 K e a 400 K, e a uma velocidade média de 0,02 m s .

Passo 1

Faaaaaaaaaaaaalaa galerinha!!

Bora continuar?!

Temos três fluidos com três propriedades diferentes, como nós não temos a temperatura nas 366 K nas tabelas nós vamos interpolar:

Precisamos calcular velocidade média, o comprimento de entrada fluidodinâmico e o comprimento de entrada térmico para cada um dos fluidos, ok?

Começando pela água, a velocidade média é dada como:

u m = m ˙ ρ π D 2 4

Sabemos que:

m ˙ = 0,01 k g s

D = 20   m m = 0,02   m

Substituindo a sua densidade e os demais dados:

u m = 0,01 k g s 962,8 k g m 3 π 0,02   m 2 4

u m = 0,033 m s

Para calcular os demais dados nós precisamos saber se o fluxo é laminar ou turbulento, portanto precisamos de Reynolds aqui:

R e D = ρ u m D μ

Substituindo nossos dados:

R e D = 962,8 k g m 3 0,033 m s 0,02   m 302,6 × 10 - 6   k g m . s = 2099,96

Como Reynolds é menor que 2300 o fluxo é laminar!!

Nestes casos o comprimento da entrada hidrodinâmica é dada por:

x h ≅ 0,05 . R e D . D

x h ≅ 0,05 . 2099,96 . 0,02   m

x h ≅ 2,01   m

E o comprimento da entrada térmica é dada por:

x t ≅ 0,05 . R e D . P r . D

x t ≅ 0,05 . 2099,96 . 1,888 . 0,02   m

x t ≅ 3,965   m

Passo 2

Agora nós faremos a mesma coisa para o óleo de motor, a velocidade média é dada como:

u m = 0,01 k g s 844,2 k g m 3 π 0,02   m 2 4

u m = 0,03 8 m s

E agora o número de Reynolds:

R e D = 844,2 k g m 3 0,03 8 m s 0,02   m 2,12 × 10 - 2   k g m . s = 30,26

Como Reynolds é menor que 2300 o fluxo é laminar!!

Nestes casos o comprimento da entrada hidrodinâmica é dada por:

x h ≅ 0,05 . R e D . D

x h ≅ 0,05 . 30,26 . 0,02   m

x h ≅ 0,03   m

E o comprimento da entrada térmica é dada por:

x t ≅ 0,05 . R e D . P r . D

x t ≅ 0,05 . 30,26 . 338 . 0,02   m

x t ≅ 10,23   m

Passo 3

Agora nós faremos a mesma coisa para a solução de Na, a velocidade média é dada como:

u m = 0,01 k g s 84 9 k g m 3 π 0,02   m 2 4

u m = 0,03 75 m s

E agora o número de Reynolds:

R e D = u m D v

Então:

R e D = 84 9 k g m 3 0,03 75 m s 0,02   m 5,797 × 10 - 7 m 2 s = 1294

Como Reynolds é menor que 2300 o fluxo é laminar!!

Nestes casos o comprimento da entrada hidrodinâmica é dada por:

x h ≅ 0,05 . R e D . D

x h ≅ 0,05 . 1294 . 0,02   m

x h ≅ 1,294   m

E o comprimento da entrada térmica é dada por:

x t ≅ 0,05 . R e D . P r . D

x t ≅ 0,05 . 1294 . 0,019 . 0,02   m

x t ≅ 24,58 × 10 - 3   m

Passo 4

Nós terminamos a letra (a) mas nos falta a (b), certo?

E o que ela pede?

Para determinar a vazão mássica, o comprimento de entrada fluidodinâmico e o comprimento de entrada térmico para a água e o óleo de motor a 300 K e a 400 K, e a uma velocidade média de 0,02 m s .

Então faremos uma nova tabelinha:

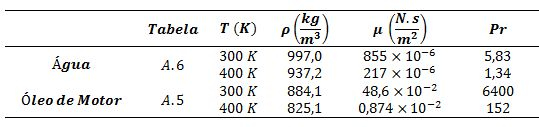
Para a água a 300K:

m ˙ = u m ρ π D 2 4

Substituindo:

m ˙ = 0,02 m s 997 k g m 3 π 0,02   m 2 4

m ˙ = 6,26 × 10 - 3 k g s

E agora o número de Reynolds:

R e D = 997 k g m 3 0,0 2 m s 0,02   m 855 × 10 - 6   k g m . s = 466,43

Como Reynolds é menor que 2300 o fluxo é laminar!!

Nestes casos o comprimento da entrada hidrodinâmica é dada por:

x h ≅ 0,05 . R e D . D

x h ≅ 0,05 . 466,43 . 0,02   m

x h ≅ 0 , 466   m

E o comprimento da entrada térmica é dada por:

x t ≅ 0,05 . R e D . P r . D

x t ≅ 0,05 . 466,43 . 5,83 . 0,02   m

x t ≅ 2,719   m

Passo 5

Para a água a 400K:

m ˙ = 0,02 m s 9 37,2 k g m 3 π 0,02   m 2 4

m ˙ = 5,88 × 10 - 3 k g s

E agora o número de Reynolds:

R e D = 937,2 k g m 3 0,02 m s 0,02   m 217 × 10 - 6   k g m . s = 1727,55

Como Reynolds é menor que 2300 o fluxo é laminar!!

Nestes casos o comprimento da entrada hidrodinâmica é dada por:

x h ≅ 0,05 . R e D . D

x h ≅ 0,05 . 1727,55 . 0,02   m

x h ≅ 1,727   m

E o comprimento da entrada térmica é dada por:

x t ≅ 0,05 . R e D . P r . D

x t ≅ 0,05 . 1727,55 . 1,34 . 0,02   m

x t ≅ 2,314   m

Passo 6

Para o óleo de motor a 300K:

m ˙ = 0,02 m s 884,1 k g m 3 π 0,02   m 2 4

m ˙ = 5 , 55 × 10 - 3 k g s

E agora o número de Reynolds:

R e D = 884,1 k g m 3 0,02 m s 0,02   m 48,6 × 10 - 2   k g m . s = 0,727

Como Reynolds é menor que 2300 o fluxo é laminar!!

Nestes casos o comprimento da entrada hidrodinâmica é dada por:

x h ≅ 0,05 . R e D . D

x h ≅ 0,05 . 0,727 . 0,02   m

x h ≅ 7,27 × 10 - 4   m

E o comprimento da entrada térmica é dada por:

x t ≅ 0,05 . R e D . P r . D

x t ≅ 0,05 . 0,727 . 6400 . 0,02   m

x t ≅ 4,653   m

Passo 7

Para o óleo de motor a 400K:

m ˙ = 0,02 m s 825,1 k g m 3 π 0,02   m 2 4

m ˙ = 5,18 × 10 - 3 k g s

E agora o número de Reynolds:

R e D = 825,1 k g m 3 0,02 m s 0,02   m 0,874 × 10 - 2   k g m . s = 37,76

Como Reynolds é menor que 2300 o fluxo é laminar!!

Nestes casos o comprimento da entrada hidrodinâmica é dada por:

x h ≅ 0,05 . R e D . D

x h ≅ 0,05 . 37,76 . 0,02   m

x h ≅ 0,037     m

E o comprimento da entrada térmica é dada por:

x t ≅ 0,05 . R e D . P r . D

x t ≅ 0,05 . 37,76 . 152 . 0,02   m

x t ≅ 5,739   m

Ufaaaaa !! Essa foi daquelas !

Resposta

  1. Á g u a :   u m = 0,033 m s         x h ≅ 2,01   m       x t ≅ 3,965   m ;

    2. Ó l e o   d e   m o t o r :   u m = 0,03 8 m s         x h ≅ 0,03   m       x t ≅ 10,23   m ;

    N a K :   u m = 0,0375 m s         x h ≅ 1,294   m       x t ≅ 24,58 × 10 - 3   m ;

  2. Á g u a   300   K :   m ˙ = 6,26 × 10 - 3 k g s         x h ≅ 0,466   m       x t ≅ 2,719   m ;

Á g u a   4 00   K :   m ˙ = 5,88 × 10 - 3 k g s         x h ≅ 1,727   m       x t ≅ 2,314   m ;

Ó l e o   d e   m o t o r   300   K :   m ˙ = 5,55 × 10 - 3 k g s         x h ≅ 7,27 × 10 - 4   m     x t ≅ 4,653   m ;

Ó l e o   d e   m o t o r   4 00   K :   m ˙ = 5 , 18 × 10 - 3 k g s         x h ≅ 0,037     m       x t ≅ 5,739   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motor elétrico fornece 3 kW à bomba da instalação da figura, que tem um rendimento de 80%. Sendo dados:a) as tubulações são de mesma seção, cujo diâmetro é de 5 cm e de mesmo material;b) k s 1 = 10
Numa certa região, há três reservatórios naturais, A, B e C, e um conjunto TB formado por uma turbina acoplada diretamente a uma bomba. As perdas de carga nas tubulações são:Entre a e b, H p a , b = 0
SAE 30W oil at 208C fl ows through a straight pipe 25 mlong, with diameter 4 cm. The average velocity is 2 m/s.(a) Is the fl ow laminar? Calculate (b) the pressure drop and(c) the power required. (d)
SAE 30 oil at 208C fl ows at 1.8 ft3/s from a reservoir into a6-in-diameter pipe. Use fl at-plate theory to estimate theposition x where the pipe wall boundary layers meet in thecenter. Compare with E
Etilenoglicol escoa com uma vazão de 0,01 kg/s através de um tubo com parede delgada e diâmetro de 3 mm. O tubo, em forma de serpentina, encontra-se submerso em um banho agitado de água que é mantido