Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 3
Água a 27°C escoa, com uma velocidade média de , através de uma tubulação com 1 km de comprimento e 0,25 m de diâmetro interno.
- Determine a queda de pressão ao longo do comprimento da tubulação e a potência de bombeamento necessária, sendo a superfície da tubulação lisa.
- Se a tubulação for de ferro fundido e sua superfície estiver limpa, determine a queda de pressão e a potência de bombeamento requerida.
- Para a condição de tubo liso, gere um gráfico da queda de pressão e da potência de bombeamento requerida para velocidades médias do fluido na faixa entre .
Passo 1
Shooow galeraa, animados ?
Bom antes de calcular a velocidade no tubo precisamos saber se o fluxo é laminar ou turbulento, certo?
Então vamos começar calculando o número de Reynolds:
Onde é a vazão mássica, o diâmetro do tubo e a viscosidade do fluido em questão, a água.
Lembrando que a velocidade é dada por:
Substituindo em Reynolds:
Quando a temperatura é de 27°C, 300K, nós vamos lá pra tabela A.6 e achar para o nosso fluido:
O problema já nos disse que:
Substituindo em Reynolds:
Como Reynolds é maior que 2300 o fluxo é turbulento !!
Passo 2
Se o fluxo é turbulento, podemos encontrar a queda de pressão de acordo com a equação:
O único dado que nós não temos aqui é o fator de atrito, e para achá-lo podemos usar a expressão para uma condição suave, ou seja, :
Substituindo o número de Reynolds:
E agora nós vamos substituir o valor na queda de pressão:
Podemos deixar esse gradiente com uma carinha melhor:
Mas a letra (a) ainda nos pediu mais uma coisa, a potência de bombeamento necessária!
Como faremos? Simples!!
Basta usarmos a expressão para a energia da bomba:
A vazão volumétrica pode ser calculada em função da área e da velocidade:
Se temos todos os dados, nos resta apenas substituir:
Terminamos a letra (a) com sucesso, bora pra (b)?
Passo 3
Na letra (b) nós iremos calcular as mesmas coisas, queda de pressão e potência, se a tubulação for de ferro fundido!!
Quando nós temos a tubulação feita de ferro fundido o único dado que vamos alterar é o fator de atrito, e para achá-lo podemos usar a Figura abaixo:
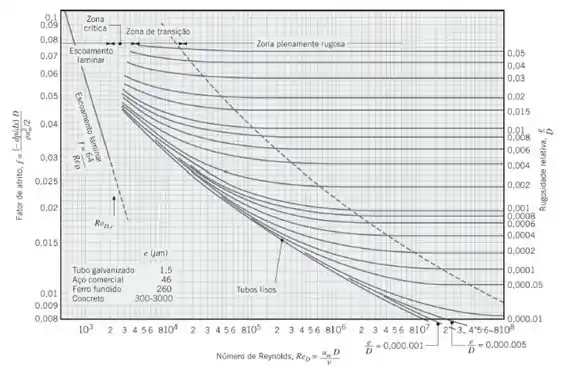
Se o Reynolds nós já temos, basta acharmos a rugosidade relativa. Para o ferro fundido a figura nos disse que:
Então:
Quando olhamos a figura podemos inferir que:
E agora nós vamos substituir o valor na queda de pressão:
Podemos deixar esse gradiente com uma carinha melhor:
E a nova pressão será:
Terminamos a letra (b) e agora vamos seguindo!!
Passo 4
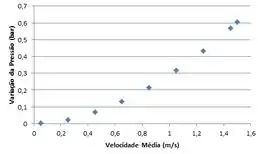
Na letra (c) nós queremos, para a condição de tubo liso (letra a), gerar um gráfico da queda de pressão e da potência de bombeamento requerida para velocidades médias do fluido na faixa entre .
Então, o que faremos?
Lançaremos estas fórmulas no software IHT, para facilitar nossa vida, e ai vamos obter os valores para as diferentes velocidades:
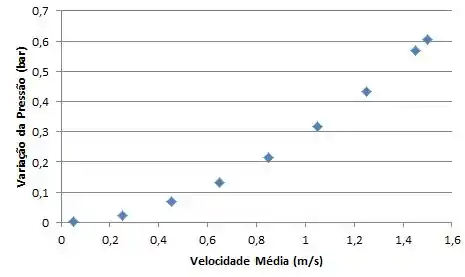
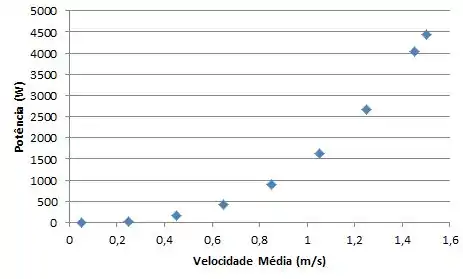
E finalizamos mais umaaa !!
