Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 19
Considere o arranjo das três superfícies negras mostrado na figura, no qual é pequena quando comparada com ou .
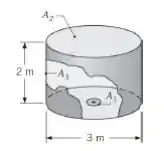
Determine o valor de . Calcule a transferência de calor por radiação líquida de para , se , e .
Passo 1
Nessa questão nós temos o arranjo de três superfícies pretas com geometrias prescritas e temperaturas da superfície. Com isso queremos encontrar o fator e a transferência líquida de calor por radiação de para .
Passo 2
Para resolver essa questão vamos assumir:
(1) As superfícies interiores se comportam como corpos negros;
(2) ;
(3) As superfícies são irradiadas uniformemente e possuem radiosidades uniformes.
Definindo o arredor como o interior da forma cilíndrica e identificando que é o anel da tampa de baixo. Aplicando a regra de soma do fator de forma, temos:
Note que,
Passo 3
Temos que,
Então,
Passo 4
Para a letra (b) temos,
Substituindo os valores,