Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 20
Uma peça longa em forma de V é tratada termicamente pela sua suspensão no interior de um forno tubular com um diâmetro de e uma temperatura de parede de . O V tem os lados com de comprimento e um ângulo de
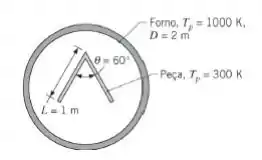
Se a parede do forno e as superfícies da peça puderem ser aproximadas por corpos negros e a peça se encontra a uma temperatura inicial de , qual é a taxa de transferência de calor por radiação líquida, por unidade de comprimento, para a peça?
Passo 1
Nessa questão nós temos o diâmetro e temperatura do forno. As dimensões e temperatura da peça suspensa. A partir disso, vamos encontrar a taxa líquida de transferência de radiação por unidade de comprimento para a peça.
Passo 2
Para resolver essa questão vamos assumir:
(1) Todas as superfícies podem ser aproximadas como corpos negros;
(2) Irradiação e radiosidade uniformes da superfície.
Por considerações de simetria, é conveniente tratar o sistema como um sistema de três superfícies que consiste nas superfícies internas do V (1), nas superfícies externas do V (2) e na parede do forno (3).
A taxa líquida de transferência de calor por radiação para a peça é então:
Passo 3
Por reciprocidade,
Onde a superfície 3 pode ser representada pela linha imaginária que transformaria o V em um triângulo e, por simetria,
Além disso,
Então,