Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 24

Uma placa circular com 500   m m de diâmetro é mantida a T 1   =   600   K e está posicionada coaxialmente a uma peça com formato cônico. O lado superior do cone é isolado termicamente. A placa e o cone, cujas superfícies são negras, estão localizados dentro de uma grande sala, cujas paredes estão a 300   K e há vácuo no seu interior.

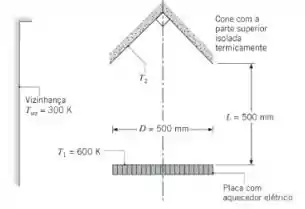
(a) Qual é a temperatura da superfície cônica, T 2 ?

(b) Qual é a potência elétrica que seria necessária para manter a placa circular a 600 K ?

Passo 1

Nessa questão nós temos uma placa circular ( A 1 ) mantida a 600   K posicionada coaxialmente com uma forma cônica ( A 2 ) cuja parte traseira é isolada. A placa e o cone são superfícies pretas e localizadas em um entorno grande e isolado a 300   K .

A partir dessas informações vamos encontrar a temperatura da superfície cônica T 2 e a energia elétrica necessária para manter a placa em 600   K .

Passo 2

Para resolver essa questão vamos assumir:

(1) Condições de estado estacionário;

(2) A placa e o cone são pretos;

(3) O cone se comporta como superfície isolada e com irradiação;

(4) Os arredores são grandes em comparação com a placa e o cone;

(5) Irradiação e radiosidade uniformes.

A placa, o cone e os arredores do entorno de três superfícies (pretas), geram o seguinte balanço de radiação no cone:

q 2 = 0 = q 23 + q 21 = A 2 F 2 3 σ T 2 4 - T 3 4 + A 2 F 2 1 σ T 2 4 - T 1 4

Onde o fator de forma F 21 pode ser determinado a partir da relação de discos paralelos coaxiais (Tabela 13.2 ou Fig. 13.5) com:

R i = r i L = 250 500 = 0,5

R j = 0,5

S = 1 + 1 + R j 2 R i 2 = 1 + 1 + 0,5 2 0,5 2 = 6 , 0

Passo 3

E note que,

F 2 ' 1 = F 21

F 12 = 1 2 S - S 2 - 4 r j r i 2 1 2 = 1 2 6 - 6 2 - 4 0,5 0,5 2 1 2 = 0,172  

Para o entorno, a regra de soma fornece,

F 2 ' 3 = 1 - F 2 ' 1 = 1 - 0,172 = 0,828

Então,

0,828 T 2 4 - 300 4 = 0 + 0,172 T 2 4 - 600 4

T 2 = 413 K

Passo 4

A potência necessária para manter a placa em T 2 segue de um balanço de radiação,

q 1 = q 12 + q 13 = A 1 F 12 σ T 1 4 - T 2 4 + A 1 F 1 3 σ T 1 4 - T 3 4

Onde,

F 12 = A 2 ' F 2 ' 1 A 1 = F 21 = 0,172

E,

F 13 = 1 - F 12 = 0,828

q 1 = π 0,5 2 4 m 2 σ 0,172 600 4 - 413 3 K 4 + 0,828 600 4 - 300 3 K 4

q 1 = 1312   W

Resposta

  1. T 2 = 413 K
  2. q 1 = 1312   W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere planos paralelos com extensão normal à página infinita como mostrado na figura. (a) Determine F 12 usando os resultados da Figura 13.4. (b) Determine F 12 usando o primeiro caso da Tabela 13
Considere duas superfícies difusas A 1 e A 2 no interior de uma cavidade esférica com raio R . Usando os métodos a seguir, deduza uma expressão para o fator de forma F 12 em termos de A 2 e R .(a) Det
Considere os retângulos paralelos mostrados na figura.Mostre que o fator de forma F 12 pode ser representado por F 12 = 1 2 A 1 [ A 1,4 F 1,4 2,3 - A 1 F 13 - A 4 F 42 ] com todos os fatores de forma
Considere o cilindro circular de diâmetro D, comprimento L e áreas A1, A2 e A3, representando as superfícies da base, interna e superior, respectivamente.(a) Mostre que o fator de forma entre a base d
Considere os planos paralelos, com extensão infinita na direção normal à página, que têm arestas opostas alinhadas conforme mostrado na figura.(a) Usando relações apropriadas do fator de forma e resul