Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 91

Considere o aspirador de pó do Problema 4-90. No caso em que , e , cri um gráfico vetorial de velocidade da metade superior do plano de a e de a . Desenhe tantos vetores quanto forem necessários para ter uma boa ideia do campo de escoamento. Observação: A velocidade é infinita no ponto e, portanto, não tente desenhar um vetor velocidade nesse ponto.

Passo 1

Temos que desenhar o campo de vetores velocidade pelo campo dado.

Assumindo que o fluxo é constante e que o fluxo opera em duas dimensões .

Gerando uma ordem de vetores no plano , com os valores dados, neste problema, podemos calcular e , das equações do Problema 4-90. Produzindo a seguinte figura:

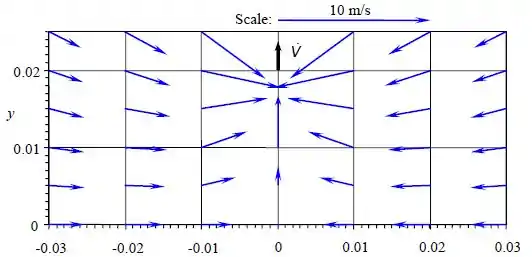
É claro que todos os vetores velocidade são sugados para o aspirador de todas as direções. Note também que não possuímos vetores velocidades de origem do chão.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um campo de escoamento em regime permanente, bidimensional e incompressível no plano x y . A taxa de deformação linear na direção x é de 2,5s - 1 . Calcule a taxa de deformação linear na dir

Um elemento de fluido bidimensional de dimensões d x e d y é transladado e distorcido como mostra a Figura P 4 - 60 durante o período de tempo infinitesimal d t = t 2 - t 1 . As componentes da velocid

Explique a relação entre vorticidade e rotacionalidade.

Um tanque cilíndrico de água gira em rotação de corpo rígido, no sentido anti-horário com relação a seu eixo vertical (Figura P 4 - 64 ) com velocidade angular ω = 360r p m . Calcule a vorticidade das

Um tanque cilíndrico de água gira com relação ao seu eixo vertical (Figura P4-64). Um sistema PIV é usado para medir o campo de vorticidade do escoamento. O valor medido da vorticidade na direção z é