Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 52

Considere uma bolha de sabão. A pressão no interior da bolha é maior ou menor do que a pressão externa?

Passo 1

A questão quer saber se a pressão P i no interior da bolha de sabão de raio R é maior ou menor do que a pressão externa P e .

Para entender melhor, termos que fazer o diagrama de corpo livre de metade da bolha. Isso será feito no próximo passo.

Passo 2

Na figura abaixo vemos metade da bolha. A força da pressão P i π ⋅ R 2 ⋅ P i se opõe à duas forças: a força que a pressão externa faz sobre a bolha π ⋅ R 2 ⋅ P e e a força da tensão superficial σ s 2 ⋅ σ s ⋅ 2 ⋅ π ⋅ R . A força da tensão superficial tem essa fórmula, porque a película de sabão forma duas superfícies. A superfície interna contribui com uma força de σ s ⋅ 2 ⋅ π ⋅ R e a superfície externa contribui com uma força igual de σ s ⋅ 2 ⋅ π ⋅ R .

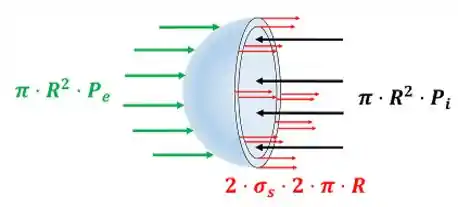
Em outras palavras, a força da pressão interna deve ser igual à soma entre a força da pressão externa e a força da tensão superficial.

π ⋅ R 2 ⋅ P i = π ⋅ R 2 ⋅ P e + 2 ⋅ σ s ⋅ 2 ⋅ π ⋅ R

Passo 3

Reorganizando a fórmula acima, criamos uma fórmula para a diferença de pressão P i - P e .

P i - P e = 4 ⋅ σ s R

Como o raio R da bolha e a tensão superficial são sempre maiores que zero, podemos dizer que:

P i - P e = 4 ⋅ σ s R 4 ⋅ σ s R > 0 ⟶ P i - P e > 0

Ou seja:

P i - P e > 0       ⟹       P i > P e

A pressão interna P i da bolha é sempre maior que a pressão externa P e da bolha!

Resposta

P i > P e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deduza os seguintes fatores de conversão: Converta uma pressão de 1 psi para kPaConverta um volume de 1 litro para galõesConverta uma viscosidade de 1 l b f · s f t 2 para N s m 2
Para uma pequena partícula de isopor (16 kg/m3) (esférica, com diâmetro d = 0,3 mm) caindo em ar padrão a uma velocidade V, a força de arrasto é dada por F D=3 π μ V d , em que μ é a viscosidade do ar
Para cada grandeza física listada, indique as dimensões usando a massa como a dimensão primária, e dê as unidades SI e Inglesas típicas: Potência Pressão Módulo de elasticidade Velocidade angularEnerg
Para o Problema 1.12, encontre a distância que as partículas viajam antes de atingirem 99% da velocidade terminal. Trace o gráfico da distância viajada em função do tempo.
Partículas muito pequenas movendo­se em fluidos são conhecidas por sofrerem uma força de arrasto proporcional à velocidade. Considere uma partícula de peso W abandonada em um fluido. A partícula sofre