Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 56

Um tubo de 1,9   m m de diâmetro é mergulhado num líquido desconhecido cuja densidade é 960   k g / m 3 . Observa-se que o líquido sobe 5   m m formando um ângulo de contato de 15 ° . Determine a tensão superficial do líquido.

Passo 1

O enunciado quer saber o valor da tensão superficial σ s de um líquido. Para responder essa pergunta, precisamos olhar para a equação 2 - 38 do livro. Ela é uma fórmula para calcular a altura h do nível do líquido no tubo em relação ao nível do líquido fora do tubo. Se a gente reorganizar essa fórmula, conseguimos criar uma equação para calcular σ s .

h = 2 ⋅ σ s ρ ⋅ g ⋅ R ⋅ cos ⁡ ϕ       ⟹       σ s = h ⋅ ρ ⋅ g ⋅ R 2 ⋅ cos ⁡ ϕ

ϕ é o ângulo de contato entre a reta tangente à superfície do líquido e a superfície do tubo.

σ s é a tensão superficial do líquido. R é o raio do tubo. g é a aceleração da gravidade. ρ é a densidade da água.

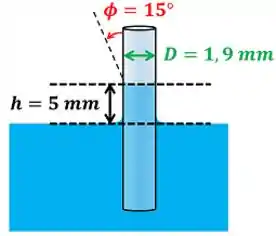
No próximo passo vamos expor e converter as unidades de todos os dados que o enunciado informou.

Passo 2

O enunciado nos informou o valor de todas as variáveis que precisamos.

R = D 2       ⟹       R = 1,9 2 ⟹       R = 0,95   m m       ⟹       R = 0,00095   m

ρ = 960   k g m 3

h = 5   m m       ⟹       h = 0,005   m

ϕ = 15 °

g = 9,81   m / s 2

No próximo passo nós vamos iniciar as contas.

Passo 3

σ s = h ⋅ ρ ⋅ g ⋅ R 2 ⋅ cos ⁡ ϕ       ⟹       σ s = 0,005 ⋅ 960 ⋅ 9,81 ⋅ 0,00095 2 ⋅ cos ⁡ 15 °       ⟹       σ s = 0,0232   N m

Resposta

σ s = 0,0232   N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Paracadagrandezafísicalistadaindiqueasdimensõesusandoaforçacomoadimensãoprimária, edêasunidadesSIeInglesas típicas: Potência Pressão Módulo de elasticidade Velocidade angularEnergiaQuantidade de movim
Para o Problema 1.14, considere que a velocidade horizontal da esportista seja 70 m/s. Como ela cai, o valor de k para a vertical permanece como antes, mas o valor para o movimento horizontal é k = 0,
Uma praticante de voo livre, com uma massa de 70 kg, pula de um avião. Sabe-se que a força de arrasto aerodinâmico agindo sobre ela é dada por FD = kV2, em que k = 0,25 N · s2/m2. Determine a velocida
Os ingleses aperfeiçoaram o arco e flecha como arma após o período Medieval. Nas mãos de um arqueiro hábil, a arma era considerada precisa a distâncias de 100 metros ou mais. Considerando que a altitu
Um fazendeiro necessita de 4 cm de chuva por semana em sua fazenda, que tem 10 hectares de área plantada. Se há uma seca, quantos galões por minuto (L/min) deverão ser bombeados para irrigar a colheit