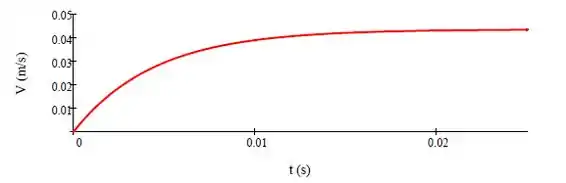
Para uma pequena partícula de isopor (16 kg/m3) (esférica, com diâmetro d = 0,3 mm) caindo em ar padrão a uma velocidade V, a força de arrasto é dada por , em que μ é a viscosidade do ar. Partindo do repouso, determine a velocidade máxima e o tempo que a partícula leva para atingir 95% dessa velocidade. Trace um gráfico da velocidade em função do tempo.

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Sabemos que a densidade da esfera é:

Como a densidade é massa sobre volume, tempos que a massa da esfera será:

Pela segunda lei de Newton, para o estado em repouso, obtemos:

Logo, a velocidade máxima será (ignorando os efeitos da flutuação):

Novamente, pela segunda lei de Newton, mas agora para um estado geral, teremos:

Resolvendo a EDO (não é nosso foco aqui a resolução de EDO), teremos:

Traçando o gráfico:

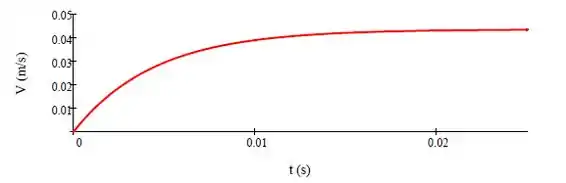
Substituindo a velocidade por 95% da máxima e substituindo os dados, teremos: