Considere o campo de escoamento dado na descrição euleriana pela expressão V = A î - B t j ^ î , em que A=2m / s , B = 2m / s 2 e as coordenadas são medidas em metros. Deduza as funções de posição lagrangiana para a partícula fluida que passou pelo ponto( x ,y )=( 1 ,1 ) no instante t=0 . Obtenha uma expressão algébrica para a trajetória seguida por essa partícula. Trace a trajetória e comparea com as linhas de corrente que passam por esse mesmo ponto nos instantes t = 0 , 1 e 2s .

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 21

Considere o campo de escoamento dado na descrição euleriana pela expressão , em que , e as coordenadas são medidas em metros. Deduza as funções de posição lagrangiana para a partícula fluida que passou pelo ponto no instante . Obtenha uma expressão algébrica para a trajetória seguida por essa partícula. Trace a trajetória e comparea com as linhas de corrente que passam por esse mesmo ponto nos instantes , e .

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Este problema nos pede a trajetória da partícula que passou pelo ponto no instante . Temos:

Para as trajetórias, temos:

Separando as variáveis:

Integrando:

Substituindo:

Com isso, teremos a trajetória ao combinarmos as equações. Logo, ela é dada por:

Para a equação das linhas de corrente:

Integrando:

Para a trajetória que passa pelo ponto :

Substituindo:

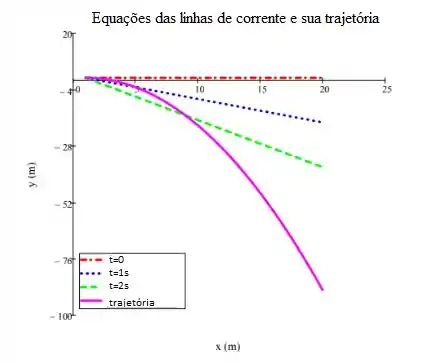
Portanto, nossos gráficos ficam assim:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um escoamento é descrito pelo campo de velocidade V =a y i+b t j , em que a=0,2s - 1 e b=0,4 m / s 2 . Em t=2s , quais são as coordenadas da partícula que passou pelo ponto (1, 2) em t = 0. Em t=3s ,

Um escoamento é descrito pelo campo de velocidade V =a i+b x j , em que a=2m / s e b=1s- 1 . As coordenadas são medidas em metros. Obtenha a equação para a linha de corrente que passa pelo ponto ( 2 ,

Um campo de velocidade é dado por V → = a x t î-b y j ^ î , em que a=0,1s - 2 e b=1s - 1 . Para a partícula que passa pelo do ponto ( x ,y )=( 1 ,1 ) no instante t=0s , trace a trajetória durante o in

Que diferença de pressão deve haver entre as pontas de um canudinho de refresco, vertical, de 15cm, para aspirar um liquido aquoso com a massa específica de 1g c m - 3 ?

Um manômetro semelhante ao que foi descrito no Exercício 1.6ª continha mercúrio em vez de água. Admita que a pressão externa seja 760 Torr e que o lado aberto esteja 10 cm mais alto que o lado conecta