Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 35

Um escoamento é descrito pelo campo de velocidade V =   a y i   +   b t j , em que a   =   0,2   s - 1 e b   =   0,4 m / s 2 . Em t   =   2   s , quais são as coordenadas da partícula que passou pelo ponto (1, 2) em t = 0. Em t   =   3   s , quais são as coordenadas da partícula que passou pelo ponto ( 1 ,   2 ) em t =   2   s ? Trace a trajetória e linha de emissão através do ponto (1, 2), e compare com as linhas de corrente através do mesmo ponto nos instantes t   =   0 , 1 , 2 e 3   s .

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Primeiro, temos que determinar a trajetória, temos:

u = d x d t = a y v = d y d t = b t

Separando as variáveis e integrando:

d x = a y   d t x - x 0 = a y 0 t - t 0 + a b 2 t 3 3 - t 0 3 3 - t 0 2 t - t 0

d y = b t   d t

y = y 0 + b 2 t 2 - t 0 2

Logo, as posições são dadas por:

x p t = x 0 + a y 0 t - t 0 + a b 2 t 3 3 - t 0 3 3 - t 0 2 t - t 0 y p ( t ) = y 0 + b 2 t 2 - t 0 2

Com isso, precisamos encontrar a posição da partícula nos instantes pedidos. Para x 0 , y 0 = ( 1,2 ) , t 0 = 0 e t = 2   s , temos:

x p t = x 0 + a y 0 t - t 0 + a b 2 t 3 3 - t 0 3 3 - t 0 2 t - t 0 = 1,9   m y p ( t ) = y 0 + b 2 t 2 - t 0 2 = 2,8   m

Para x 0 , y 0 = ( 1   ,   2 ) e t 0 = 2 s e t = 3   s :

x p t = x 0 + a y 0 t - t 0 + a b 2 t 3 3 - t 0 3 3 - t 0 2 t - t 0 = 1,4   m y p t = y 0 + b 2 t 2 - t 0 2 = 3   m

Passo 2

Para as linhas de emissão, temos:

x t 0 = x 0 + a y 0 t - t 0 + a b 2 t 3 3 - t 0 3 3 - t 0 2 t - t 0 y t 0 =   y p ( t ) = y 0 + b 2 t 2 - t 0 2

Passo 3

Agora, precisamos encontrar a equação das linhas de corrente. Para isso, temos que:

v u = d y d x = b t a y

Separando as variáveis e integrando:

b a   t   d x = y   d y y 2 - y 0 2 2 = b t a ( x - x 0 )  

Subsituindo x 0 = 1 e y 0 = 2 , ficamos com a solução da seguinte forma:

y = 4 t x - 1 + 4

Passo 4

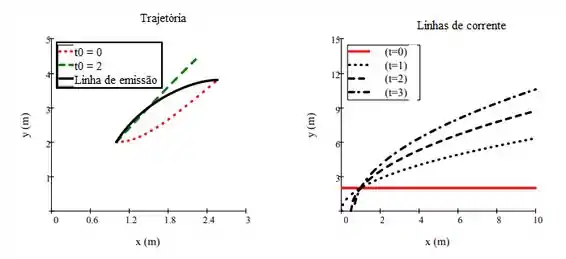
Por fim, nossos gráfcmos ficam assim:

Resposta

x p t = 1,9   m y p ( t ) = 2,8   m

x p t = 1,4   m

y p t = 3   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No viscosímetro da figura, o cilindro externo gira com uma rotação de 100r p m constante. O cilindro interno é oco, sua parede tem espessura desprezível e está preso a um calibrado à torção. Esse cili
Num tear, o fio é esticado passando por uma fieira e é enrolado num tambor com velocidade constante, como mostra a figura. Na fieira, o fio é lubrificado e tingido por uma substância. A máxima força q
O eixo da figura, ao girar, provoca a rotação do tambor. Este enrola a corda, que levanta um peso de 10N com uma velocidade constante de 0,5m / s . O fluido existente entre o eixo e o tambor tem μ = 0
Dois discos são dispostos coaxialmente face a face, separados por um filme de óleo lubrificante de espessura ε pequena. Aplicando-se um momento no disco 1 , ele inicia um movimento em torno de seu eix
No sistema da figura, o corpo cilíndrico de peso G desce com velocidade constante v = 2m / s , fazendo o eixo girar. Dados μ = 10 - 3N ⋅ s / m 2 ; L = 2 / πm ; D e = 50,2c m ; D i = 50c m ; d = 10c m