Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 84b

Considere uma cavidade cilíndrica de diâmetro D = 100 mm e profundidade L = 50 mm, cujas parede lateral e fundo são difusas e cinzas com uma emissividade de 0,6 e estão a uma temperatura uniforme de 1500 K. O topo da cavidade é aberto e exposto a uma vizinhança que é grande e encontra-se a 300 K.

  1. Calcule a transferência de calor radiante líquida saindo da cavidade, tratando o fundo e a parede lateral da cavidade como duas superfícies separadas (qB).

Passo 1

Agora, diferente do que fizemos na letra a não vamos mais considerar a cavidade como uma superfície única!

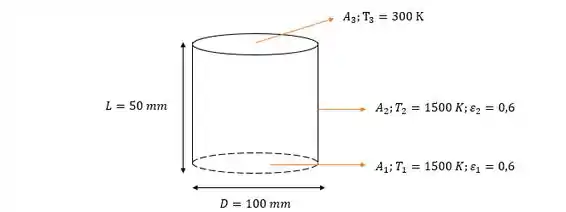
Mas ainda queremos saber a quantidade de calor que sai da cavidade!!

Concorda comigo que:

q 3 = - ( q 1 + q 2 )

É por ai que a gente vai!!!

Da equação 13.20 do livro, podemos fazer:

q 3 = A 3 F 31 J 3 - J 1 + A 3 F 32 ( J 3 - J 2 )

Passo 2

As superfícies 1 e 3 são discos paralelos coaxiais, para descobrir F 13 , vamos usar as relações da tabela 13.2 , depois usamos outras relações pra descobrir F 31 e F 32 :

R 1 = R 3 = r L = 100 2 50 = 1

S = 1 + 1 + R 2 2 R 1 2 = 1 + 1 + 1 2 1 2 = 3

Para calculr F 12 :

F 13 = 1 2 S - S 2 - 4 D 2 D 1 2 1 2

Substituindo:

F 13 = 1 2 3 - 3 2 - 4 100 100 2 1 2 = 0,382

Pela regra da reciprocidade:

A 1 F 13 = A 3 F 31

Mas A 1 = A 3 , então F 13 = F 31 e pela regra da soma:

F 32 = 1 - 0,382 = 0,6 18

Passo 3

Agora precisamos achar J 1 e J 2 ! Para isso:

E b i - J i 1 - ε i ε i A i = ∑ j = 1 N J i - J j A i F i j - 1

Para A 1 :

E b 1 - J 1 1 - ε 1 ε 1 A 1 = J 1 - J 2 A 1 F 12 - 1 + J 1 - J 3 A 1 F 13 - 1

Como a superfície 3 é uma abertura, então, J 3 = σ T 3 4 , E b 1 = E b 2 = σ T 4 e podemos também cortar A 1

E b 1 - J 1 1 - ε 1 ε 1 = J 1 - J 2 F 12 - 1 + J 1 - J 3 F 13 - 1

Pela simetria, F 12 = F 23 = 0,618 , substituindo, temos:

5,67 × 10 - 8 × 1500 4 - J 1 1 - 0,6 0,6 = J 1 - J 2 0,618 - 1 + J 1 - 5,67 × 10 - 8 × 300 4 0,382 - 1

Simplificando:

2,5 J 1 - 0,618 J 2 = 430,741     ( 1 )

Agora para A 2 :

E b 2 - J 2 1 - ε 2 ε 2 = J 2 - J 1 F 21 - 1 + J 2 - J 3 F 23 - 1

Pela regra da reciprocidade:

A 2 F 21 = A 1 F 12

Logo:

F 21 = A 1 A 2 F 12 = π D 2 4 π D L F 12 = D 4 L F 12 = 100 4 × 50 × 0,618 = 0,309

E pela regra da simetria:

F 21 = F 23

Substituindo:

5,67 × 10 - 8 × 1500 4 - J 2 1 - 0,6 0,6 = J 2 - J 1 0,309 - 1 + J 2 - 5,67 × 10 - 8 × 300 4 0 , 309 - 1

Simplificando:

- 0,309 J 1 = 2,118 J 2 = 430,708       ( 2 )

Resolvendo ( 1 ) e ( 2 ) achamos:

J 1 = 230,491   W / m 2

J 2 = 234,654   W / m 2

Passo 4

Podemos finalmente achar q 3 :

q 3 = 7,854 × 10 - 3 × 0,381 459,3 - 230,491 + 7,854 × 10 - 3 × 0,618 ( 459,3 - 234,654 )

Achamos:

q 3 = 1840   W

Uhuuul!!

Resposta

q 3 = 1840   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um recinto cilíndrico cuja altura é duas vezes o diâmetro de sua base. Determine o fator de forma da superfície lateral deste recinto cilíndrico para sua superfície da base.
Um cone circular de diâmetro D é posicionado em um eixo comum com disco circular, também de diâmetro, D, a uma distância L, como mostrado na Fig. P13-18. Com uma área hipotética ( A 3 ) correspondente
130 - O número de fatores de forma que precisam ser avaliados diretamente para um recinto de 10 superfícies é(A) 1 (B) 10 (C) 22 (D) 34 (E) 45
126 - Considere duas esferas concêntricas com diâmetros de 12c m e 18c m formando um recinto cujas temperaturas de superfície são 300K . Assumindo que as superfícies são negras, a troca de radiação lí
117 - Duas placas quadradas, com os ladosaebba são coaxiais e paralelas entre si, como mostrado na Fig. P13-117, e são separadas pela distânciacentro a centrode L .O fator de forma da radiação da plac