Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 88

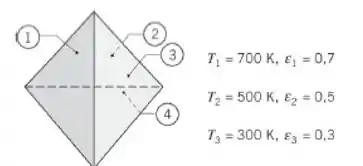
Considere a cavidade composta por quatro superfícies cinzas e difusas, com todos os lados iguais, mostrada na figura. As temperaturas de três superfícies são especificadas, enquanto a quarta encontra-se termicamente isolada e pode ser tratada como uma superfície rerradiante. Determine a temperatura da superfície rerradiante (4).

Passo 1

Falaaaaaa galerinha !!

Vamos seguindo?

Bom, nós queremos a temperatura da superfície 4, certo? Como ela exibe o comportamento de um quadro negro nós podemos relacionar a temperatura com a potência emissiva e a radiosidade

J 4 = E b 4 = σ T 4 4

Já sabemos que:

σ = 5,67 × 10 - 8 W m 2 K 4

Então precisamos achar J 4 !!

Quando nós conhecemos a temperatura superficial, podemos usar a seguinte equação para as quatro superfícies, assumindo que a área é 1 m²:

E b 1 - J 1 1 - ε 1 ε 1 = J 1 - J 2 1 F 12 + J 1 - J 3 1 F 13 + J 1 - J 4 1 F 13

E b 2 - J 2 1 - ε 2 ε 2 = J 2 - J 1 1 F 21 + J 2 - J 3 1 F 23 + J 2 - J 4 1 F 23

E b 3 - J 3 1 - ε 3 ε 3 = J 3 - J 1 1 F 3 1 + J 3 - J 2 1 F 3 2 + J 3 - J 4 1 F 3 4

E b 4 - J 4 1 - ε 4 ε 4 = J 4 - J 1 1 F 4 1 + J 4 - J 2 1 F 4 2 + J 4 - J 3 1 F 4 3

Deu pra assustar, não é? Mas vamos ver o que sabemos !

ε 1 = 0 , 7

ε 2 = 0 , 5

ε 3 = 0 , 3

Só precisamos do fator forma e das radiosidades,ok?

Passo 2

Agora que vocês já sabem que nós vamos ter que resolver estas 4 equações simultaneamente para achar as radiosidades !!

Vamos começar achando a potência emissiva das três superfícies que conhecemos as temperaturas:

T 1 = 7 00   K

T 2 = 5 00   K

T 3   =   300   K

Sabendo que:

E b 1 = σ T 1 4

E b 2 = σ T 2 4

E b 3 = σ T 3 4

E substituindo:

E b 1 = 5,67 × 10 - 8 W m 2 K 4 7 00   K 4 = 13614   W m 2  

E b 2 = 5,67 × 10 - 8 W m 2 K 4 5 00   K 4 = 3544   W m 2

E b 3 = 5,67 × 10 - 8 W m 2 K 4 3 00   K 4 = 459 W m 2

Só precisamos do fator de forma, certo?

Como as superfícies são simétricas podemos dizer que:

F i j = 1 3

Então todos os fatores de forma valerão 1 3 !

Passo 3

Vamos começar substituindo para a superfície 1:

13614 - J 1 1 - 0,7 0,7 = J 1 - J 2 1 1 3 + J 1 - J 3 1 1 3 + J 1 - J 4 1 1 3

13614 - J 1 = 0,14286   3 J 1 - J 2 - J 3 - J 4

13614 = 1,42857 J 1 - 0,14286   J 2 - 0,14286 J 3 - 0,14286 J 4                       ( 1 )

Para a superfície 2:

3544 - J 2 1 - 0 , 5 0 , 5 = J 2 - J 1 1 1 3 + J 2 - J 3 1 1 3 + J 2 - J 4 1 1 3

3544 - J 2 = 0 , 33333   3 J 2 - J 1 - J 3 - J 4

3544 = - 0,33333   J 1 + 2 J 2 - 0,33333   J 3 - 0,33333   J 4                       ( 2 )

Para a superfície 3:

459 - J 3 1 - 0,3 0,3 = J 3 - J 1 1 1 3 + J 3 - J 2 1 1 3 + J 3 - J 4 1 1 3

459 - J 3 = 0 , 77778   3 J 3 - J 1 - J 2 - J 4

459 = - 0,77778   J 1 - 0,77778   J 2 + 3 , 333333 J 3 - 0,77778   J 4                       ( 3 )

Para a superfície 4, lembrando que E b 4 = J 4 :

J 4 - J 4 1 - ε 4 ε 4 = J 4 - J 1 1 1 3 + J 4 - J 2 1 1 3 + J 4 - J 3 1 1 3

0 = 3 J 4 - J 1 - J 2 - J 3                       ( 4 )

Agora vamos utilizar um software de sua preferência para resolver as 4 equações simultaneamente:

J 1 = 11,613 W m 2

J 2 = 6045 W m 2

J 3 = 6106 W m 2

J 4 = 7922 W m 2

Agora que sabemos J 4 podemos simplesmente substituir na fórmula do Passo 1:

7922 W m 2 = 5,67 × 10 - 8 W m 2 K 4 T 4 4

T 4   =   611,4   K

Ufaaaa !! Terminamos mais uma !!

Resposta

T 4   =   611,4   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um recinto infinitamente longo com três faces laterais com comprimentos de 5c m , 3c m e 4c m . O fator de forma a partir do lado de 5c m para o lado de 4c m é ( a )0,3 ( b )0,4 ( c )0,5 (
103 - Considere dois discos paralelos coaxiais de diâmetros a e b , mostrado na Fig. P13-103.Para essa geometria, o fator de forma do disco menor para o disco maior pode ser calculado por F = 0,5 B A
99 - Considere um invólucro cilíndrico com A 1 , A 2eA 3 representando as bases interna, e superior e as superfícies laterais, respectivamente.Usando o comprimento de diâmetro, K = L / D , determine (
101 - Um secador é moldado como um duto semicilíndrico longo de diâmetro de 1,5m .A base do secador é ocupada por materiais encharcados com água e mantidos e mantida a uma temperatura de 370K com uma
103 - Considere dois discos paralelos coaxiais de diâmetros a e b , mostrado na Fig. P13-103.Para essa geometria, o fator de forma do disco menor para o disco maior pode ser calculado por F = 0,5 B A