Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 99

99 - Considere um invólucro cilíndrico com  A 1 , A 2   e   A 3  representando as bases interna, e superior e as superfícies laterais, respectivamente. Usando o comprimento de diâmetro, K = L / D , determine (a) a expressão para o fator de forma a partir da superfície lateral para F 33  em K e (b) o valor do fator de forma F 33  para  L = D .

Passo 1

Vamos relembrar algumas relações matemáticas antes de prosseguir com problema:

Área de superfície da base,  A 1 = π 4 D 2 .

Área de superfície do topo,  A 2 = π 4 D 2 .

Superfície da superfície lateral,  A 3 = π D L .

Relação comprimento do diâmetro, K = L D  .

Passo 2

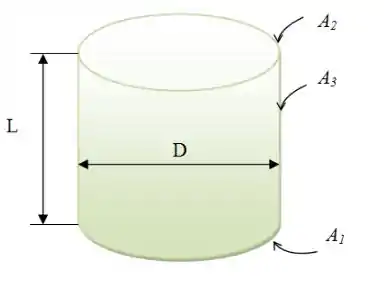
Passo 3

a)

Nas expressões de fator de forma para algumas geometrias comuns de tamanho finito temos que:

Para discos paralelos coaxiais,

F 12 = 1 + 1 - 4 R 2 + 1 2 R 2

Onde,  R = D 2 L

Reescrevendo R em termos de K, temos R = 1 2 K .

Passo 4

Portanto, o fator de forma da base para o topo, é escrito como:

F 12 = 1 + 1 - 4 R 2 + 1 2 R 2

= 1 + 1 - 4 1 2 K 2 + 1 2 1 2 K 2

= 1 + 1 - 4 4 K 2 + 1 2 4 K 2

= 1 + 1 - 1 K 2 + 1 1 2 K 2

= 1 + 2 K 2 - 2 K 2 1 K 2 + 1    

= 1 + 2 K 2 - 2 K 2 1 + K 2 K 2    

= 1 + 2 K 2 - 2 K 2 K K 2 + 1    

= 1 + 2 K 2 - 2 K K 2 + 1    

= 1 + 2 K K - K 2 + 1

Passo 5

Ao usar a regra da reciprocidade, o fator de forma da superfície superior para a superfície base pode ser expresso como:

F 21 = A 1 A 2 F 12

= 1 × 1 + 2 K K - K 2 + 1

= 1 + 2 K K - K 2 + 1

Como as áreas das superfícies base e superior são iguais, os fatores de forma também são os mesmos.

Passo 6

O fator de forma da base para a superfície lateral é determinado pela aplicação da regra de soma;

F 11 + F 12 + F 13 = 1  

F 13 = 1 - F 11 - F 12

Como a superfície da base é plana temos que o F 11 = 0 . Substituindo  F 12 , o fator de forma da base para a superfície lateral pode ser expresso como:

F 13 = 1 - 0 - 1 + 2 K K - K 2 + 1  

= 2 K K - K 2 + 1

Passo 7

Ao usar a regra de reciprocidade, o fator de forma da superfície lateral para a superfície base pela superfície superior pode ser expresso como:

F 31 = F 32 = A 1 A 3 F 13

= π 4 × D 2 π D × L × 2 K 2 2 K 2 + 1 - 2 K 2

= 1 4 K × 2 K K 2 + 1   - 2 K 2

= 1 2 K 2 + 1 - K

Passo 8

O fator de forma da superfície lateral para si é determinado por: F 33 + F 31 + F 32 = 1 .

Reescrevendo a equação, obteremos:

F 33 = 1 - 2 × F 31

= 1 - 2 × 1 2 K 2 + 1 - K

F 33 = 1 - K 2 + 1 - K

Passo 9

b)

Para L = D temos que o valor de  K = 1 . Portanto, o fator de visualização  F 33 pode ser calculado como:

F 33 = 1 - 1 2 + 1 - 1

= 2 - 2

F 33 = 0,589

Resposta

A) F 33 = 1 - K 2 + 1 - K

B)   F 33 = 0,589

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o Problema 9.93 com N = 4 finas folhas de alumínio (εf = 0,07), igualmente espaçadas ao longo do espaço de 50 mm, formando assim cinco espaços de ar individuais cada um com 10 mm de espessur
Um longo aquecedor na forma de bastão, com diâmetro D1 = 10 mm e emissividade ε1 = 1,0, encontra-se posicionado coaxialmente a um refletor semicilíndrico isolado termicamente com diâmetro D2 = 1 m. Um
Um gerador de vapor é constituído por um feixe alinhado de tubos, cada um com diâmetro externo D = 10 mm e comprimento L = 1 m. Os passos longitudinal e transversal são SL = ST = 20 mm, enquanto os nú
Um aquecedor a gás natural utiliza a combustão em um leito poroso de material catalítico para manter uma placa cerâmica, com emissividade εc = 0,95, a uma temperatura uniforme de Tc = 1000 K. A placa
Um orifício com fundo plano e 6 mm de diâmetro é perfurado até uma profundidade de 24 mm em um material cinza e difuso, que tem uma emissividade de 0,8 e uma temperatura uniforme de 1000 K. Determine