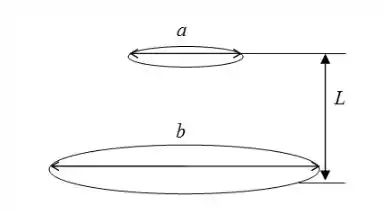
103 - Considere dois discos paralelos coaxiais de diâmetros e , mostrado na Fig. P13-103. Para essa geometria, o fator de forma do disco menor para o disco maior pode ser calculado por
Onde, , e . O diâmetro, emissividade e temperatura são , e , respectivamente, para o disco de , e , e para o disco . A distância entre os dois discos é .
- Calcule e
- Calcule a taxa líquida de transferência de calor por radiação entre os discos e em regime permanente.
- Suponha que outro disco (infinitamente) grande , de espessura desprezível e, é inserido entre os discos de e de tal forma que é paralela e equidistante de ambos os discos. Calcule a taxa líquida de transferência de calor por radiação entre os discos e e entre os discos e , em operação permanente.
Passo 1
Dados fornecidos:
Diâmetro do disco a,
Emissividade do disco a,
Temperatura superficial do disco a,
Diâmetro do disco b,
Emissividade do disco b,
Temperatura da superfície do disco b,
Distância centro a centro,
Passo 2
Passo 3
a)
O fator de forma da superfície para a superfície é dado como:
Onde,
Passo 4
Portanto, o fator de visualização pode ser calculado como:
Passo 5
O fator de visualização da superfície para a superfície a pode ser calculado usando a regra de reciprocidade. A área do disco 'a' e do disco 'b' pode ser calculada como:
Passo 6
Portanto, o fator de visão calculado como:
Passo 7
b)
A taxa líquida de transferência de calor por radiação entre as superfícies pode ser determinada como:
Portanto, o calor perdido devido à radiação é .
Passo 8
c)
Nesse caso, temos um disco infinitamente grande, ou seja, e a emissividade do disco é . Como o disco é infinitamente grande, a visualização é fatorada em . Portanto, .
Ao aplicar um balanço de energia, temos que:
Substituindo pelos valores conhecidos, temos:
Como sabemos que ,
A taxa de transferência de calor é mais alta na parte (c) porque o disco grande c é capaz de coletar toda a radiação emitida pelo disco a. Portanto, não está atuando como um escudo de radiação.
Resposta
- e
- O calor perdido devido à radiação é .
- A taxa de transferência de calor é mais alta na parte (c) porque o disco grande c é capaz de coletar toda a radiação emitida pelo disco a. Portanto, não está atuando como um escudo de radiação.