Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 93
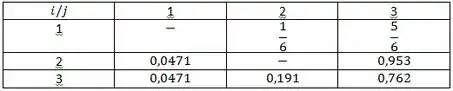
Um pequeno forno é constituído por uma caixa cúbica, de lado L = 0,1 m, como mostrado. O piso da caixa é constituído por um aquecedor que fornece P = 400 W. As paredes restantes perdem calor para a vizinhança fora do forno, fato que mantém suas temperaturas a T3 = 400 K. Um objeto esférico, com diâmetro D = 30 mm, encontra-se posicionado no centro do forno. Algum tempo após a esfera ser posicionada no interior do forno, sua temperatura é de T1 = 420 K. Todas as superfícies têm emissividade igual a 0,4.
- Determine os seguintes fatores de forma: F12, F13, F21, F31, F23, F32, F33.
- Determine a temperatura do piso e a taxa de transferência de calor líquida por radiação deixando a esfera. A esfera está em condições de regime estacionário?
Passo 1
Shoow de bola galerinhaaa !!
Vamos continuar?
Aqui nós queremos começar achando os fatores de forma, não é?
Nós já achamos dois facilmente, devido a simetria para a esfera (1) o seu fator de forma com relação às seis paredes será:
Usando a reciprocidade podemos achar três fatores, vamos começar por e :
Lembrando que:
Então:
Fazendo o somatório para a superfície 2:
E agora nós podemos chegar ao terceiro fator forma calculado pela reciprocidade:
Substituindo:
Com mais um somatório para a superfície 3:
Ihuuuul !!
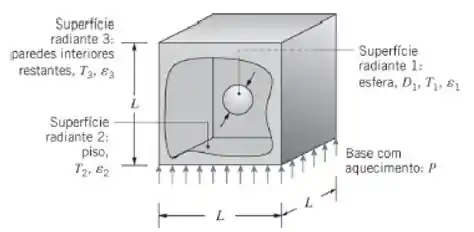
Vamos só por em uma tabelinha?
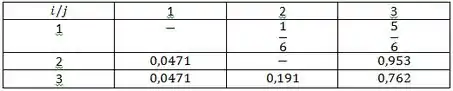
E chegamos ao fim da letra (a) !!
Passo 2
Na letra (b) nós queremos achar a temperatura do piso e a taxa de transferência de calor líquida por radiação deixando a esfera, não é? Como o problema nos disse nós temos duas superfícies, certo?
Para a taxa de radiação liquida transferida em uma superfície podemos usar a seguinte relação:
Onde é a potência emissiva, a radiosidade, a área e a emissividade da superfície i.
Vamos dar uma olhada nas equações abertas?
Nós já sabemos que:
Agora o que nós precisamos é achar as radiosidades!
Mas para isso precisamos achar as potências emissivas:
Lembrando que:
Então:
Então nós precisamos dos fatores de forma para conseguirmos calcular as radiosidades !!
Passo 3
Agora nós vamos substituir tudo nas equações do Passo 2:
Resolvendo as duas equações simultaneamente:
Para a taxa de transferência de calor nós precisamos somente aplicar a primeira parte da igualdade para a superfície 1:
Então nós temos uma transferência liquida para a superfície 1, certo? Se é assim ela não está em estado estacionário !!
Passo 4
Agora nós só precisamos da temperatura da superfície 2, mas como ela está relacionada à potência emissiva vamos começar achando ela, ok?
Para isso vamos usar a relação do Passo 2:
Substituindo:
E suando a relação entre a temperatura e a potência emissiva:
E substituindo:
Shooow galerinha !! Finalizamos mais umaa !!
