Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 47 c
Considere as cavidades formadas por um cone, um cilindro e uma esfera que têm o mesmo tamanho de abertura (d) e dimensão principal (L), como mostrado na figura.
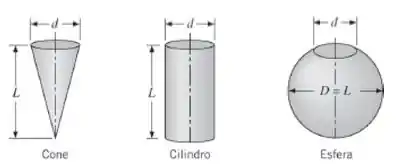
(c) Para cada cavidade e emissividades da parede de εp = 0,5, 0,7 e 0,9, represente graficamente εef como uma função da razão entre a dimensão principal e o tamanho da abertura, L/d, para valores dessa razão entre 1 e 10.
Passo 1
Vamos láa!!
A gente vai pegar as equações de para cada forma e vamos plotar os gráficos!!
Cone:
Variando entre e :
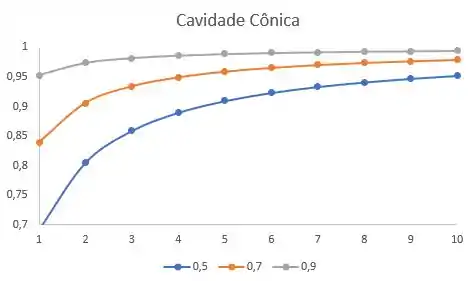
Agora pra o cilindro:
Plotando:
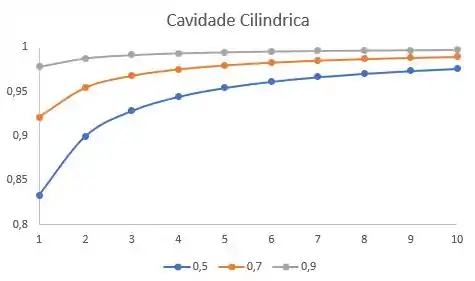
Esfera:
Lembrando que aqui, vamos considerar , beleza?!
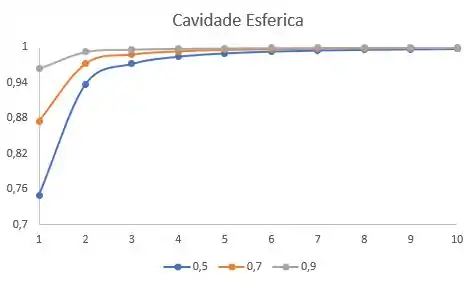
Aweeee!!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
O método dos “filamentos cruzados” de Hottel [7] fornece um meio simples para calcular fatores de forma entre superfícies que têm extensão infinita em uma direção. Para duas destas superfícies (a) com
Considere as seguintes fendas, cada uma com largura W, que foram usinadas em um bloco de material sólido.Para cada caso, obtenha uma expressão para o fator de forma da fenda com relação à vizinhança f
Deduza expressões para o fator de forma F12 associado aos arranjos a seguir. Expresse os seus resultados em termos de A1, A2 e qualquer outra área de superfície hipotética apropriada, assim como do fa
Determine F12 e F21 para as seguintes configurações usando o teorema da reciprocidade e outras relações básicas do fator de forma. Não utilize tabelas ou gráficos.Duto longo:Pequena esfera com área A1
Dois objetos convexos estão no interior de um grande recipiente, no qual há vácuo. As paredes do recipiente são mantidas a T 3=300K . Os objetos têm a mesma área, igual a 0,2m 2 , e a mesma emissivida