O método dos “filamentos cruzados” de Hottel [7] fornece um meio simples para calcular fatores de forma entre superfícies que têm extensão infinita em uma direção. Para duas destas superfícies (a) com visões sem obstrução uma da outra, o fator de forma tem a forma

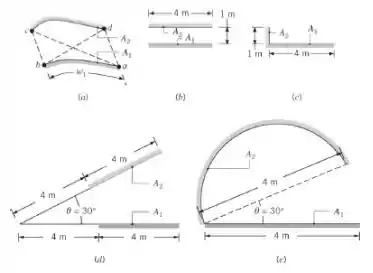
Use esse método para determinar os fatores de forma nas figuras (b) a (e). Compare os seus resultados com aqueles obtidos nos gráficos, nas expressões analíticas e nas relações de fatores de forma apropriadas.

Para resolver essa questão vamos assumir placas infinitas em extensão na direção normal para a página. O método dos filamentos cruzados é aplicável a superfícies de extensão infinita em uma direção com uma visão desobstruída uma da outra.

Placas paralelas: a partir do esquema, as bordas e as distâncias diagonais são,

Com como a largura da placa, encontramos,

Usando a Fig. 13.4 com e encontramos . Além disso, usando a primeira relação da Tabela 13.1,

Onde, e e encontramos:

Placas perpendiculares com uma aresta comum: a partir do esquema, a aresta e as distâncias diagonais são,

Com como a largura das placas horizontais, encontramos,

A partir da terceira relação da Tabela 13.1, com me , encontramos,

Placas em ângulo entre si: A partir do esquema, as distâncias da borda e da diagonal podem ser calculadas da seguinte forma:

Por simetria,

Com isso, encontramos:

Semi-círculo e placa em ângulo um com o outro: As distâncias da borda e da diagonal são,

Com isso, encontramos:

O mesmo resultado pode ser encontrado usando as relações de fator de exibição na Tabela 13.1. Como a radiação que passa de a deve passar por 3, . Na Tabela 13.1, segunda entrada,