Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 01
Determine F12 e F21 para as seguintes configurações usando o teorema da reciprocidade e outras relações básicas do fator de forma. Não utilize tabelas ou gráficos.
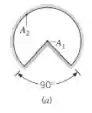
- Duto longo:
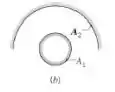
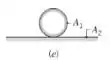
- Pequena esfera com área A1 sob um hemisfério concêntrico com área A2 = 2A1
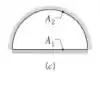
- Duto longo. Qual o valor de F22 nesse caso?
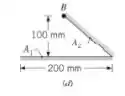
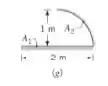
- Longas placas inclinadas (o ponto B encontra-se diretamente acima do centro de A1)
- Esfera apoiada sobre um plano infinito
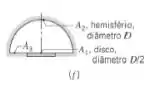
- Configuração hemisfério-disco
- Canal aberto longo
Passo 1
Fala aí! Beleza? Vamos resolver essa questãozinha juntos? Simmm!!
Bom, nosso enunciado pediu pra não usar tabelas ou gráficos… Então precisamos determinar e , com base na relação de reciprocidade, que a equação 13.3 nos apresenta, e com base na regra de soma, que é a equação 13.4 … Agora vamos para cada letrinha de uma vez, ok?
Primeiro a letra a, ela nos apresenta um duto longo, nesse caso temos, por análise:
E por reciprocidade:
Partiu letra b!
Passo 2
Agora nós temos Pequena esfera, sob um hemisfério concêntrico… Pro regra da soma, temos que:
E sendo , por causa da simetria, temos:
E por reciprocidade:
Show! Vamos para a letra c!
Passo 3
Agora temos um duto longo novamente, mas ele é apenas meia esfera… Vamos ter por análise:
Por reciprocidade:
E por regra da soma, vamos ter que:
Partiu letra d!
Passo 4
Agora nós temos Longas placas inclinadas, por regra da soma temos:
E se, por simetria, :
E por reciprocidade vamos ter:
Pronto! Vamos para letra e!
Passo 5
Bom, temos agora uma esfera em um plano infinito, por regra da soma, nós temos:
Mas , por simetria, então:
E por reciprocidade vamos ter:
Mas como , tende a infinito, pois estamos em um plano infinito:
Partiu letra f!
Passo 6
Bom, agora nós temos um hemisfério-disco, de diâmetro , por análise temos:
E por regra da soma, vamos ter que:
E por reciprocidade, teremos duas conclusões, a primeira é que:
A segunda conclusão é que:
E novamente usando a regra da soma, mas agora para :
Prontinho!! Pra fechar agora vamos para a letra g!
Passo 7
Agora nós temos um canal aberto e longo, que forma meia circunferência… Usando a regra da soma teremos:
Mas como , vamos ter que:
E por reciprocidade, temos:
Uhul! Finalmente acabamos!
Resposta
- Passo 1;
- Passo 2;
- Passo 3;
- Passo 4;
- Passo 5;
- Passo 6;
- Passo 7.