Considere as condições associadas ao Problema , mas agora com um processo convectivo no qual .

(a) Em coordenadas , esboce as distribuições de temperaturas para as seguintes condições: condição inicial , condição de regime estacionário , e dois tempos intermediários. Identifique características importantes das distribuições, especialmente a

localização da temperatura máxima e o gradiente de temperatura em .

(b) Em coordenadas , esboce o fluxo térmico nas posições e , ou seja, e , respectivamente. Identifique características importantes dos históricos dos fluxos.

(a)

Tendo tudo isso em mente vamos a nossa letra (a), o gráfico de em função do espaço. Para isso vamos escrever nossa lei de Fourier (equação ).

Como nossa condução é unidimensional e há geração de energia, temos:

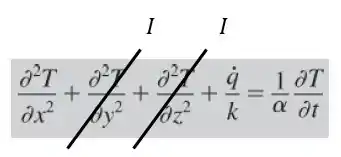
Assim nossa equação fica:

Como quanto nossa parede não aqueceu nossa superfície então a temperatura é , assim nossa equação fica:

Agora pra nossas condições de contorno, na superfície contraria ao fluído, não tem fluxo de calor, já que está isolada. Na outra superfície o fluxo de calor vai ser máximo, ou seja:

Resolvendo a E.D.O para esse sistema temos:

Assim nosso gráfico fica:

No instante nossa parede está começando a aquecer mas a perca de calor é na parede em contato com o fluído faz que a temperatura fique abaixo da temperatura inicial, num instante posterior a parede está aquecida o suficiente devido a geração de calor a ponto de dissipar calor pro ambiente nas proximidades da superfície em contato com o fluído e em a temperatura já atingiu um patamar constante em todas as seções da parede.

(b) Bem nosso problema nos pede uma representação gráfica da distribuição do fluxo de temperatura ao longo do tempo, usar nossos cálculos da letra (a) para nossa

Assim nosso gráfico fica assim.

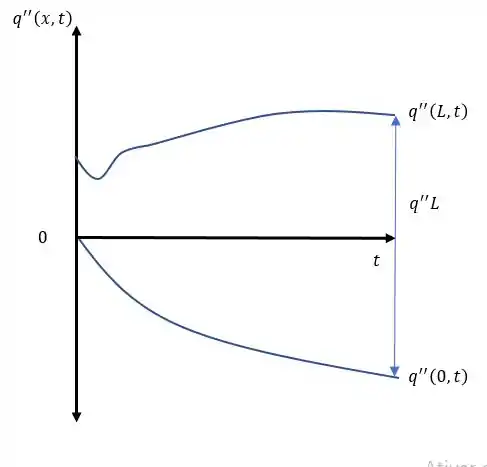
Vamos lá! Quando o processo nossa parede começa a aquecer, mas a superfície em contato com o fluído perde calor logo e essa perca de calor reduz a diferença de temperatura entre a superfície e a parede, como a equação que rege a transferência por convecção é dada por:

Nosso fluxo vai sofrer uma pequena queda no começo do processo devido essa redução na diferença de temperatura, então aumenta até se tornar constante no regime permanente.

Já na outra superfície ela vai decair gradualmente até manter uma constância no regime permanente, o sentido do fluxo é ilustrado na imagem a baixo.

Isso é tudo pessoal! \o/