Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 79

Considere as condições do Problema 9.9, mas agora encare o problema como um envolvendo convecção natural em canais verticais formados por placas paralelas. Qual é o espaçamento ótimo, S , entre as aletas? Para esse espaçamento e os valores especificados para t e W , qual é a taxa de transferência de calor nas aletas?

Passo 1

Primeiro passo é buscarmos dos dados do exercício 9.9, aqui eu os trouxe, junto a um esboço:

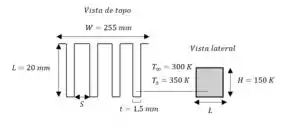
Como todo problema de transferência de calor, precisamos encontrar as propriedades do fluido em questão, ou seja, vamos começar determinando a temperatura de filme para entrar na tabela:

T f = T s + T ∞ 2 = 300 + 350 2 = 325   K

Portanto, da tabela A-4 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.)...

ν = 18,41 × 10 - 6 m 2 s ,   k = 0,0282 W m ∙ K ,   α = 26,1 × 10 - 6 m 2 s ,   P r = 0,703

Passo 2

Bom, o primeiro parâmetro solicitado para determinarmos é o melhor espaçamento S entre as aletas.

Do enunciado, temos que a física do problema é uma transferência de calor por convecção natural entre placas paralelas verticais.

O que facilita muito pra nós, pois basta consultarmos os parâmetros na tabela 9.3 (Incropera -Fundamentos de Transferência de Calor e Massa - 7°Ed.).

Portanto, para placas isotérmicas simétricas:

S o t i = 2,71 R a S S 3 H - 1 4

S o t i = 2,71 g β T S - T ∞ α ν H - 1 4

S o t i = 2,71 9,81 m s 2 325   K - 1 50   K 26,1 × 10 - 6 m 2 s 18,4 × 10 - 6 m 2 s 0,15   m - 1 4 = 7,12   m m

Passo 3

O exercício além disso, nos pede para determinar a taxa de transferência de calor nas aletas, ou seja, iremos utilizar a equação abaixo para isso:

q = 2 N h - ( L × H ) ( T s - T ∞ )

Onde temos que:

N = W S o t i + t = 355   m m 7,12   m m + 1,5   m m ≈ 41

Passo 4

Para determinar nosso coeficiente convectivo, precisamos antes determinar o número de Nusselt, onde que para convecção natural em canais verticais para placas paralelas, em condições isotérmicas:

N u - S = C 1 R a S S L 2 + C 2 R a S S L 1 2 - 1 2

Da tabela 9.3 (Incropera -Fundamentos de Transferência de Calor e Massa - 7°Ed.).

C 1 = 576

C 2 = 2,87

Portanto...

R a S S L = g β T s - T ∞ S 4 α ν H = 9,81 m s 2 325 K - 1 50   K 7,12 × 10 - 3   m 4 25,4 × 10 - 6 m 2 s 18,4 × 10 - 6 m 2 s 0,15   m

R a S S L = 53,2

Passo 5

Determinando o número de Nusselt...

N u - S = 576 53,2 2 + 2,87 53,2 1 2 - 1 2 = 0,204 + 0,393 - 1 2 = 1,29

Determinando o coeficiente convectivo...

N u - S = h - S k

h - = 1,29 0,0282 W m ∙ K 0,0072   m = 5,13 W m 2 ∙ K

Passo 6

Por fim, agora podemos determinar a taxa de transferência de calor nas aletas...

q = 2 N h - ( L × H ) ( T s - T ∞ )

q = 82 5,13 W m 2 ∙ K 0,02   m × 0,15   m 50 K

q = 63,1   W

Resposta

O espaçamento ótimo S é:

S o t i = 7,12   m m

A taxa de transferência de calor nas aletas é:

q = 63,1   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Alguém alega que o espaço de ar em uma janela de painel duplo reforça a transferência de calor da casa por causa das correntes de convecção natural que ocorrem no espaço de ar e, por isso, recomenda q
Duas esferas concêntricas com diâmetros de 15 cm e 25 cm ão separadas por ar a 1 atm de pressão. As temperaturas da superfície das duas superfícies aprisionando o ar são T 1 = 350K e T 2 = 275K , resp
Mostre que a resistência térmica de um espaço fecahdo retangular pode ser expressa como R = L c A kN u , onde k é a condutividade térmica do fluido no espaço fecahdo.
O que a condutividade efetiva do espaço fechado representa? Como é a relação entre condutividade efetiva e condutividade térmica relacionada ao número de Nusselt?
Considere uma caixa alta retangular de 3 m de altura composta por duas superfícies separadas por intervalo de ar de 0,1 m a 1 atm. Se as temperaturas da superfície em todo o espaço de ar são 30°C e –1