Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 2
Considere condução unidimensional, em regime estacionário, no objeto axissimétrico mostrado a seguir, que está isolado termicamente ao longo de seu perímetro.
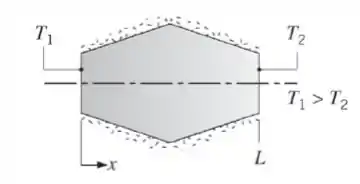
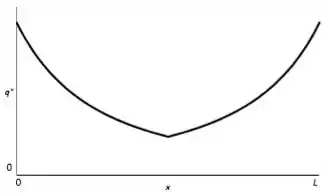
Se as propriedades permanecerem constantes e não ocorrer geração interna de calor, esboce a distribuição de fluxos térmicos, , e a distribuição de temperaturas, T(x). Explique as formas das curvas propostas. Como as suas curvas dependem da condutividade térmica do material?
Passo 1
Beleza galerinha, vamos lá! Para as condições prescritas, resulta da conservação de energia, Eq. 1.12c, que para um volume de controle diferencial:
Ou,
Passo 2
Isso significa que é independente de . Portanto,
onde é a área da secção transversal perpendicular à direcção x. Portanto, o fluxo de calor deve ser inversamente proporcional à área da secção transversal. O raio do objeto primeiro aumenta e depois diminui linearmente com , então a área da seção transversal aumenta e depois diminui como . A distribuição do fluxo de calor resultante é esboçada abaixo.
Passo 3
Para encontrar a distribuição da temperatura, podemos usar a lei de Fourier:
Portanto, o gradiente de temperatura é negativo e sua magnitude é proporcional ao fluxo de calor. A temperatura diminui mais rapidamente onde o fluxo de calor é maior e mais lentamente onde o fluxo de calor é menor.
