Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 71
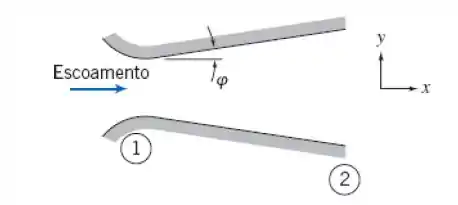
Considere o difusor de parede plana, mostrado na Fig. P.9.71. Primeiro, considere que o fluído é não viscoso. Descreva a configuração do escoamento, incluindo a distribuição de pressão, quando o ângulo do difusor, , é aumentado a partir de zero grau (paredes paralelas). Segundo, modifique sua descrição para levar em conta efeitos da camada limite. Qual fluído (não viscoso ou viscoso) terá, em geral, maior pressão de saída?
Passo 1
Vamos analisar as duas situações onde há crescimento de : onde há efeitos de viscosidade e e onde não há. E com base nisso, entender em qual situação temos a maior pressão de saída.
O que a gente precisa lembrar:
- quando a seção de escoamento uniforme aumenta, a velocidade diminui, e vice-versa
- quando a velocidade diminui, a pressão aumenta, e vice-versa
Vamos lá!
Passo 2
Na primeira situação temos o fluído sem viscosidade.
O que acontece é que quando , não há variação de pressão entre as extremidades do tubo, mas quando esse ângulo aumenta, pela conservação de massa:
Temos que a velocidade vai diminuir na saída, logo a pressão vai aumentar.
Passo 3
Na segunda situação, onde há viscosidade, já temos diferença de pressão em , por causa da camada limite, nesse caso, a velocidade é maior na saída e a pressão é menor, considerando que área de escoamento uniforme vai diminuindo.
Quando aumentamos esse ângulo, a velocidade de saída vai diminuir, porque a área de saída está aumentando. Logo, a pressão vai aumentar.
Se for muito alto, a velocidade pode diminuir bruscamente até haver separação entre o fluído e as paredes.
Passo 4
Como na situação onde não há viscosidade (não há camadas limite), a área da seção de escoamento uniforme é maior no final, podemos dizer que aí há maior pressão.
Resposta
Há maior pressão de saída no fluído não viscoso.