Considere as distribuições de temperaturas em regime estacionário no interior de uma parede composta pelos Materiais e para os dois casos mostrados. Não há geração interna e o processo de condução é unidimensional.

Responda as perguntas a seguir para os dois casos. Qual material tem a maior condutividade térmica? A condutividade térmica varia de forma significativa com a temperatura? Caso positivo, como? Descrever a distribuição de fluxos térmicos através da parede composta. Se a espessura e a condutividade térmica dos dois materiais forem dobradas e as temperaturas nas extremidades permanecerem as mesmas, qual seria o efeito na distribuição de fluxos térmicos?

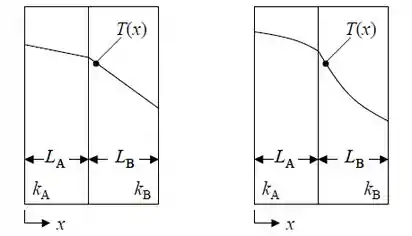
Caso . As distribuições de temperaturas nos dois materiais são lineares, como mostrado.

Caso . As distribuições de temperaturas nos dois materiais não são lineares, como mostrado.

Vamos lá! agora precisamos analisar nossos sistemas para o regime permanente. Utilizando a lei de Fourier de condução, para os materiais e , assim temos:

No regime permanente nosso fluxo será constante então temos:

Vamos lá, dividindo nosso fluxo de pelo fluxo temos:

Pois o gradiente de temperatura é maior na segunda metade, ou seja o material oferece menor resistência a passagem de calor!

Tendo em vista que o fluxo de calor pela parede é constante, a lei de Fourier dita que para materiais de baixa condutividade térmica, para manter a o fluxo constante o gradiente precisa ser grande.

Imaginem o fluxo como um veículo que você está, e você precisa derrubar um muro com uma batida, se o muro for de concreto, vamos precisar de um carro grande, de preferência um caminhão, então basicamente é isso que precisamos pra manter o fluxo constante, uma “força grande”, essa “força” vem da diferença de temperatura!

Pro caso O gradiente de temperatura é linear então a diferença do coeficiente de condutividade térmica não deve variar muito com a temperatura.

Pro caso O gradiente de temperatura pro material em temperaturas baixa é menor, ou seja, o coeficiente aumenta significantemente para temperaturas menores, podemos ver isso na curva que tende a ser uma reta “deitada” com o tempo, ou seja não tem troca de calor.

Isso é tudo pessoal! \o/