Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 2.Problemas - Ex. 25
25 – Uma haste composta consiste de dois diferentes materiais, A e B, cada um com comprimento de 0,5L.
A condutividade térmica do material A é metade da do material B, isto é, kA/kB=0,5. Esboce a distribuição de temperatura, T(x), e fluxo de calor, qx”, em estado estacionário. Assumir propriedades constantes e sem geração de interna de calor para ambos os materiais.
Passo 1
Para conseguirmos esboçar a distribuição de temperatura e também o fluxo de calor, precisaremos de uma expressão matemática em função de x (comprimento do material).
Para isso vamos utilizar a equação global do calor, aplicada a uma parede plana.
Passo 2
Lembrando da eq. do calor, que em coordenadas cartesianas (x, y, z), é a seguinte:
Onde,
-x, y e z são as coordenadas cartesianas de um sistema tridimensional;
-T é a temperatura;
-k é a condutividade térmica;
-, é a geração volumétrica de calor;
-cp é o calor especifico;
-ρ é a densidade;
-t é o tempo.
Os termos da eq. são:
-Condução de calor na direção x:
-Condução de calor na direção y:
-Condução de calor na direção z:
-Geração de energia na forma de calor:
-Variação temporal da temperatura no volume de controle:
Passo 3
Agora vamos estabelecer as condições acerca do processo para aplicarmos na eq. do calor e reduzirmos ela.
Pelo enunciado, sabemos que o processo ocorre em estado estacionário, então não variação temporal,
Também sabemos que não tem geração de energia, assim
Pela figura, podemos assumir que ocorre uma condução unidimensional, apenas na direção x, assim
Portanto a eq. do calor é simplificada para:
Passo 4
Com essa equação, conseguimos determinar uma expressão de T(x).
Resolvendo a equação diferencial, Eq2:
Tirando a constante de dentro do parêntese, pois as propriedades são constantes:
Integrando em relação a x
Integrando novamente em relação a x
Passo 5
Vemos que achamos uma expressão em que T é linear em relação a x, assim a distribuição de temperatura nos materiais seguirá um padrão linear.
A distribuição de temperatura pode ser esboçada da seguinte forma:
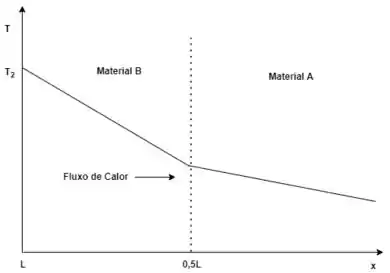
Veja que a temperatura varia linearmente com uma inclinação menor no material A, isso porque este material possui uma condutividade térmica menor em relação ao material B.
Passo 6
Agora para o fluxo de calor, vamos relembra da Lei de Fourier:
A Lei de Fourier para um processo difusivo ocorrendo de forma unidimensional é:
Assim, vamos derivar a Eq3 para encontrar uma expressão para q’’:
Derivando,
Assim, você pode ver que o fluxo de calor é constante ao longo do comprimento de cada material, sendo que para o material A, o fluxo de calor será a metade do fluxo de calor do material B.
O esboço da distribuição pode ser a seguinte:
Resposta
