Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 167
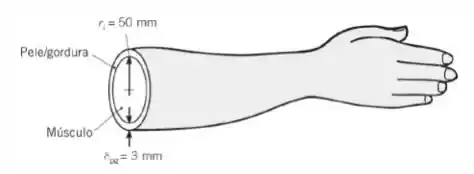
Considere a transferência de calor em um antebraço, que pode ser aproximado por um cilindro de músculo de raio (desprezando a presença dos ossos), com uma camada externa de pele e gordura com espessura de . Há geração de calor metabólica e perfusão no interior do músculo. A taxa de geração de calor metabólica, a taxa de perfusão, a temperatura arterial, e as propriedades do sangue, do músculo e da camada de pele/gordura são as mesmas do Exemplo 3.12. O ambiente e a vizinhança são os mesmos do ambiente ar no Exemplo 3.12.
- Escreva a equação do calor-bio em coordenadas radiais. Escreva as condições de contorno que expressam simetria no eixo central do antebraço e temperatura especificada na superfície externa do músculo. Resolva a equação diferencial e aplique as condições de contorno para encontrar uma expressão para a distribuição de temperaturas. Note que as derivadas das funções de Bessel modificadas são dadas na Seção 3.6.4.
- Iguale o fluxo térmico na superfície externa do músculo ao fluxo térmico através da camada pele/gordura e para o ambiente, para determinar a temperatura na superfície externa do músculo.
- Encontre a temperatura máxima no antebraço.
Passo 1
Opa! Fala aí! Partiu resolver essa questão! Ela parece ser grande, mas a gente dá conta!
Bom, ela faz referência ao exemplo 3.12, e nos dá três letrinhas para resolver… Vamos começar pelo começo então… A letra a, que que a gente resolva a equação diferencial e depois aplique as nossas condições de contorno, então vamos fazer isso com a essa equação aqui olha:
Estamos trabalhando com condições de simetria na linha central, então nossa temperatura fica assim, olha só:
E se a gente tem um excesso de temperatura com essa cara aqui:
Então nossa equação vai ficar assim:
Agora considerando nosso , vamos ficar com:
E se temos como condição de contorno que , vamos ficar com:
E se usar a condição onde , vamos ficar com:
Agora pra fechar, vamos lá:
Show! Agora é partir pra letra b!
Passo 2
Agora precisamos da temperatura na superfície externa do músculo, e vamos fazer isso igualando os fluxos térmicos!
Se colocamos a taxa de calor por unidade de comprimento, em relação a resistência total, vamos ter o seguinte:
Opa! Então temos duas equações para encontrar o , vamos igualar as duas, beleza?
Mas precisamos achar a resistência total, né?
Então vamos prosseguir!
Show!
Passo 3
Mas ainda tá faltando coisa!!
Vamos achar quem falta:
Primeiro o :
Agora sim! Vamos primeiro isolar a temperatura e depois substituir todo mundo que a gente tem, beleza?
Pra achar os valores de e de , vamos consultar a tabela B.5, tranquilo?
Lá a gente encontra que:
Vamos colocar isso na nossa equação, beleza?
Show! Fechamos a letra b!
Passo 4
Vamos resolver a letra c pra acabar, ok?
Então precisamos encontrar a temperatura máxima do antebraço, e isso vai ser quando e o nosso :
Prontinho! Conseguimos!