Seja a condução unidimensional em uma parede plana composta. Sua superfície externa está exposta a um fluido a , com um coeficiente convectivo de . Na parede intermediária há geração uniforme de calor a uma taxa , enquanto não existe geração nas paredes e . As temperaturas nas interfaces são e .
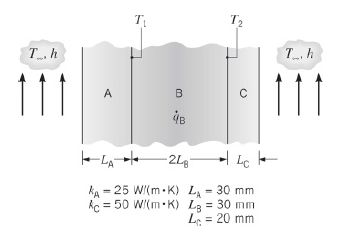
(a) Supondo resistências de contato desprezíveis nas interfaces, determine a taxa volumétrica de geração de calor e a condutividade térmica .
(b) Represente graficamente a distribuição de temperaturas, mostrando suas características importantes.
(c) Considere condições que correspondam à perda de refrigerante na superfície exposta do material . Determine e e represente a distribuição de temperaturas ao longo de todo o sistema.
Passo 1
Nessa questão, queremos encontrar (a) geração volumétrica de calor e condutividade térmica para o material B, (b) gráfico da distribuição de temperatura, (c) e , bem como distribuições de temperatura correspondentes à perda da condição do líquido de refrigeração, onde na superfície A.
PRESSUPOSTOS:
(1) Transferência de calor unidimensional em estado estacionário;
(2) Resistência de contato desprezível nas interfaces;
(3) Geração uniforme em B; zero em A e C.
DADOS FORNECIDOS:
Temperatura do fluido externo:
Coeficiente convectivo:
Temperaturas na interface AB:
Temperaturas na interface BC:
Condutividade térmica da parede A:
Condutividade térmica da parede C:
Espessura da parede A:
Espessura da parede B:
Espessura da parede C:
Passo 2
(a) Para resolver essa questão, vamos começar desenhando o circuito térmico para a parede A. Assim temos:

Com o circuito térmico desenhado, podemos dizer que a transferência de calor por unidade de área da parede A pode ser dada pela seguinte relação:
Aqui, é a temperatura na interface, é a temperatura ambiente, é o coeficiente de transferência de calor por convecção, é a espessura da parede A e é a condutividade térmica da parede A. Substituindo os termos da equação acima pelos dados fornecidos, temos o seguinte:
Passo 3
Agora, vamos desenhar o circuito térmico para a parede C. Assim temos:

Com o circuito térmico desenhado, podemos dizer que a transferência de calor por unidade de área da parede C pode ser dada pela seguinte relação:
Aqui, é a temperatura na interface, é a temperatura ambiente, é o coeficiente de transferência de calor por convecção, é a espessura da parede C e é a condutividade térmica da parede C. Substituindo os termos da equação acima pelos dados fornecidos, temos o seguinte:
Passo 4
Podemos desenhar as taxas de fluxo de energia para a parede B da seguinte forma:
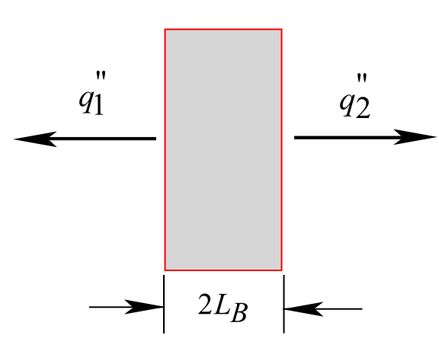
Em que, ao aplicarmos a equação de energia na parede B vamos obter o seguinte:
Aqui, é a energia que entra na parede B, é a energia que sai da parede B, é a energia gerada na parede B e é a energia acumulada. Temos que não ocorre acúmulo e nem entrada de energia, logo esses termos são iguais a zero, temos também que a energia que são é . Assim, temos o seguinte:
Podemos dizer também que a energia gerada na parede B pode ser dada pela seguinte relação:
Aqui, é a geração volumétrica de calor na parede e é a espessura da parede B. Substituindo, temos:
Portanto, a geração volumétrica de calor na parede B é .
Passo 5
Para determinar , podemos usar a equação da distribuição de temperatura para parede plana (Eq. 3.46) na parede B e a distribuição de fluxo de calor na parede B. Ou seja:
e
Passo 6
Podemos agora derivar a distribuição de temperatura, substituir na equação da distribuição de fluxo de calor na parede B e aplicar as condições de contorno para encontrar . Derivando, temos:
Substituindo temos o seguinte:
Aplicando a condição de contorno, temos que quando , . Substituindo, temos:
Substituindo os termos da equação acima pelos dados obtidos temos o seguinte:
Portanto, a condutividade térmica da parede B é .
Passo 7
(b) Queremos representar graficamente a distribuição de temperaturas nas paredes A, B e C. Temos que a distribuição de temperatura na parede B é dada pela seguinte equação:
Também temos que a distribuição de temperaturas para uma parede plana sem geração de energia pode ser dada pela equação 3.3. Então, para a parede A temos o seguinte:
e para a parede C, temos o seguinte:
Passo 8
Podemos encontrar usando a seguinte expressão:
Substituindo os termos da equação acima pelos dados fornecidos, temos o seguinte:
Podemos encontrar usando a seguinte expressão:
Substituindo os termos da equação acima pelos dados fornecidos, temos o seguinte:
Agora, vamos substituir todos os dados obtidos anteriormente, nas expressões de distribuição de temperaturas das paredes A, B e C. Assim, temos o seguinte:
Passo 9
Agora, usando as equações acima, podemos plotar o gráfico. Assim temos:
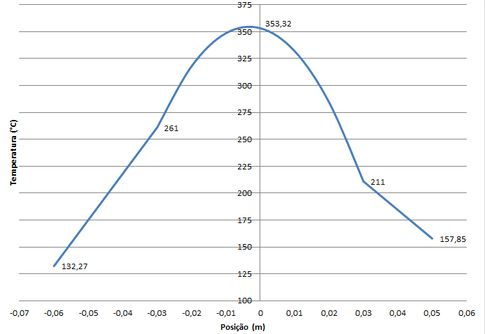
Características importantes:
(1) a distribuição é quadrática em B, mas não simétrica; linear em A e C;
(2) Como as condutividades térmicas dos materiais são diferentes, existem descontinuidades em cada interface;
(3) Comparando os gradientes em e , podemos perceber que .
Passo 10
(c) Temos que a taxa de transferência de calor no lado A é igual a zero, isso é devido ao coeficiente de transferência de calor ser igual a zero ao longo da superfície A exposta ao ambiente. Assim, a taxa de transferência de calor do lado C igual à taxa de geração de calor em B. Ou seja:
Passo 11
Podemos então encontrar a temperatura da superfície exposta ao ambiente da parede C usando a seguinte equação:
Substituindo os termos da equação acima pelos dados obtidos, temos:
Agora, Podemos encontrar a temperatura da interface entre as paredes B e C usando a seguinte relação:
Substituindo os termos da equação pelos dados obtidos, temos o seguinte:
Portanto a temperatura na interface BC é .
Passo 12
Agora, vamos encontrar a temperatura na interface entre as paredes A e B. Para isso, vamos usar a distribuição de temperatura na parede B e também a distribuição de fluxo de calor na parede B.
e
Podemos agora derivar a distribuição de temperatura, substituir na equação da distribuição de fluxo de calor na parede B e aplicar as condições de contorno para encontrar . Derivando, temos:
Substituindo temos o seguinte:
Aplicando a condição de contorno, temos que quando , . Substituindo, temos:
Temos que não a taxa de transferência de calor no lado A é igual a zero, ou seja, . Substituindo os termos da equação acima pelos dados obtidos temos o seguinte:
Portanto a temperatura na interface AB é .
Passo 13
Podemos encontrar usando a seguinte expressão:
Como foi dito acima, . Assim temos:
Da mesma forma que fizemos na letra (b), agora, vamos substituir todos os dados obtidos anteriormente, nas expressões de distribuição de temperaturas das paredes A, B e C. Assim, temos o seguinte:
Passo 14
Agora, usando as equações acima, podemos plotar o gráfico. Assim temos:
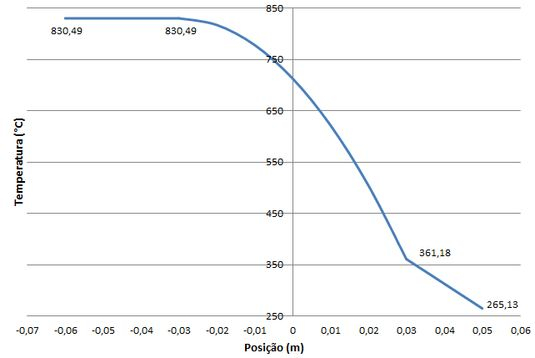
Resposta
(a)
(c)