Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 157

Considere o enunciado e o diagrama do Problema 4.155. Considere que em t = 0 , quando o bloco de mass m = 5   k g está em x = 0 , ele seja posto em movimento para a direita com velocidade u = 10   m / s . O jato de água tem velocidade v = 20   m / s e área A = 100   m m 2 . Calcule o tempo requerido para reduzir a velocidade do bloco a u = 2,5   m / s . Trace o gráfico da posição do bloco v e r s u s o tempo. Calcule a posição final do bloco em repouso. Explique por que esse é um repouso momentâneo.

Passo 1

Considerações Iniciais:

  1. Escoamento em estado estacionário;
  2. Escoamento incompressível;
  3. Escoamento com velocidade constante ( V 1 = v - u   e   V 2 = v + u ) ;
  4. Escoamento uniforme.
  5. Força de resistência desprezível.

Passo 2

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

F = F S + F B - ∫ V C a r ρ d ∀ = ∂ ∂ t ∫ V C V ρ   d ∀ + ∫ S C V ( ρ V ) d A = 0

Como estamos analisando um sistema x , temos:

F S x + F B x - ∫ V C a r f x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não há forças de campo atuando no sistema e não a resistência, então, F B x = F S x = 0 :

- ∫ V C a r x ρ d ∀ = ∂ ∂ t ∫ V C u ρ   d ∀ + ∫ S C u ( ρ V ) d A

Não temos a variação das propriedades com o tempo, então:

∂ ∂ t = 0

Assim:

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Passo 3

- ∫ V C a r x ρ d ∀ = ∫ S C u ( ρ V ) d A

Então:

- a r x ⋅ m = u 1 - ρ V 1 A + u 2 - ρ V 2 A + u 3 ⋅ m 3 ˙

u 1 = v - u ;

u 2 = - ( v + u ) ;

u 3 = 0 ;

A expressão de aceleração se dá:

- a r x ⋅ m = u 1 - ρ V A + u 2 - ρ V A + u 3 ⋅ m 3 ˙

- a r x ⋅ m = ρ A [ - v - u 2 + v + u 2 ]

a r x = - 4 u v ρ A m

Passo 4

Sendo a r x = d u d t :

d u d t = - 4 u v ρ A m

d u u = - 4 v ρ A m d t

∫ u 0 u d u u = - ∫ 0 t 4 v ρ A m d t

Integrando, obtemos:

ln ⁡ u u 0 = - 4 v ρ A m t

u = u 0 e - 4 v ρ A m t

Passo 5

Calculando tempo requerido para reduzir a velocidade do bloco a u = 2,5   m / s .

Dados:

u 0 = 10   m / s ;

v = 20   m / s ;

A = 10 - 4 m 2 ;

u = 2,5   m / s /

ρ = 1000   k g / m 3 ;

m = 5   k g .

Temos:

u = u 0 e - 4 v ρ A m t

t = - m 4 v ρ A ⋅ ln ⁡ u u 0

t = - 5 4 ⋅ 20 ⋅ 1000 ⋅ 10 - 4 ⋅ ln ⁡ 2,5 10 = 0,866   s

Passo 6

Para calcularmos a posição final do bloco em repouso, temos que saber que:

u = d x d t

Assim

d x d t = u 0 e - 4 v ρ A m t

d x = u 0 e - 4 v ρ A m t d t

∫ 0 x d x = ∫ 0 t u 0 e - 4 v ρ A m t d t

Integrando, obtemos:

x = m u 0 4 v ρ A ⋅ 1 - e - 4 v ρ A m t

Utilizando os dados do Passo 5:

x = 5 ⋅ 10 4 ⋅ 20 ⋅ 1000 ⋅ 10 - 4 ⋅ 1 - e - 4 ⋅ 20 ⋅ 1000 ⋅ 10 - 4 ⋅ 0,866 5 = 4,69   m

Passo 7

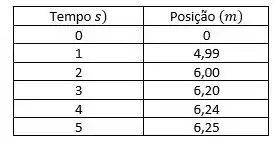
Traçando o gráfico da posição do bloco v e r s u s o tempo

Resposta

t = 0,866   s

x = 4,69   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma série de pás curvas atingidas por um jato contínuo de água com velocidade constante, V = 86,6m / s . O jato sai de um bocal de 50m m de diâmetro e as pás se movem com velocidade constant
Considere novamente o jato e o carrinho do Problema 4.149, mas inclua uma força de arrasto aerodinâmico proporcional ao quadrado da velocidade do carrinho, F D = k u 2 , com k = 2,0N s 2 / m 2 . Deduz
Resolva o Problema 4,141, considerando o bloco/pá deslizando sobre uma película de óleo em vez de estar em contato direto com a superfície. Admita que a resistência ao movimento seja proporcional à ve
Um carrinho, com uma pá defletora fixa, está livre para rolar sobre uma superfície nivelada. A massa do conjunto carrinho/pá é m = 5k g e seua velocidade inicial é u 0 = 5m / s . Em t = 0 , a pá é ati
Resolva o Problema 4.141, considerando o bloco/pá deslizando sobre uma película de óleo em vez de estar em contato direto com a superfície. Admita que a resistência ao movimento seja proporcional à ve